
Формула за допустима грешка (Съдържание)
- Формула за грешка
- Примери на формула за допустима грешка (с шаблон на Excel)
- Калкулатор на формула за грешка
Формула за грешка
В статистиката изчисляваме интервала на достоверност, за да видим къде ще падне стойността на данните от извадката. Диапазонът от стойности, които са под и над статистическата извадка в интервал на доверие, е известен като Margin of Error. С други думи, това е основно степента на грешка в статистическата извадка. Колкото по-голям е границата на грешка, толкова по-малка ще бъде увереността в резултатите, тъй като степента на отклонение в тези резултати е много висока. Както подсказва името му, границата на грешката е диапазон от стойности над и под действителните резултати. Например, ако получим отговор в проучване, при което 70% от хората са отговорили „добро“ и допустимата грешка е 5%, това означава, че като цяло 65% до 75% от населението смятат, че отговорът е „добър“,
Формулата за допустима грешка -
Margin of Error = Z * S / √n
Където:
- Z - Z резултат
- S - Стандартно отклонение на население
- n - Размер на пробата
Друга формула за изчисляване на границата на грешка е:
Margin of Error = Z * √((p * (1 – p)) / n)
Където:
- p - пробна пропорция (част от пробата, която е успешна)
Сега, за да намерите желания z резултат, трябва да знаете интервала на доверие на извадката, тъй като оценката Z зависи от това. По-долу е дадена таблица, за да видите съотношението на доверителен интервал и z оценка:
| Доверителен интервал | Z - Резултат |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
След като знаете интервала на доверие, можете да използвате съответната стойност z и да изчислите границата на грешката от там.
Примери на формула за допустима грешка (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на маржа на грешката.
Можете да изтеглите този шаблон за марж на грешка тук - шаблон на полето за грешкаФормула за граница на грешка - Пример №1
Да речем, че провеждаме анкета, за да видим каква е оценката на оценките, която получават студентите в университета. Избрахме на случаен принцип 500 ученици и поискахме оценката им. Средната стойност е 2, 4 от 4, а стандартното отклонение е 30%. Да приемем, че интервалът на доверие е 99%. Изчислете граница на грешка.
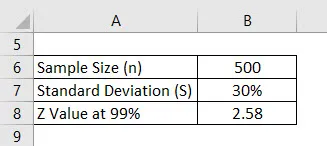
Решение:
Маржът на грешката се изчислява по формулата, дадена по-долу
Погрешка = Z * S / √n
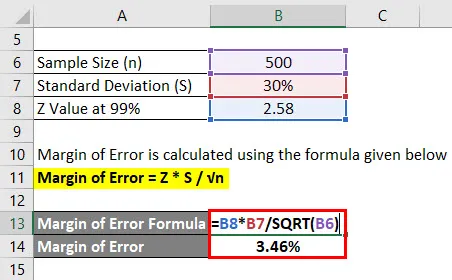
- Погрешка = 2, 58 * 30% / √ (500)
- Погрешка = 3, 46%
Това означава, че с 99% увереност средната оценка на студентите е 2, 4 плюс или минус 3, 46%.
Формула на граница на грешка - пример №2
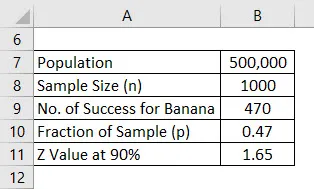
Да речем, че пускате на пазара нов здравен продукт, но сте объркани кой аромат ще хареса хората. Вие сте объркани между аромат на банан и аромат на ванилия и сте решили да проведете проучване. Населението ви за това е 500 000, което е вашият целеви пазар и от това решихте да попитате мнението на 1000 души и това ще бъде извадката. Да приемем, че интервалът на доверие е 90%. Изчислете граница на грешка.
Решение:
След като анкетата е направена, разбрахте, че 470 души харесват аромата на банан, а 530 са поискали аромат на ванилия.
Маржът на грешката се изчислява по формулата, дадена по-долу
Погрешка = Z * √ ((p * (1 - p)) / n)
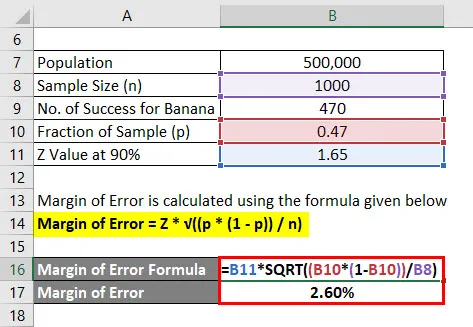
- Погрешка = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Погрешка = 2, 60%
Така че можем да кажем, че с 90% увереност, че 47% от всички хора харесват аромат на банан плюс или минус 2, 60%.
обяснение
Както беше обсъдено по-горе, допустимото ниво на грешка ни помага да разберем дали размера на извадката от вашето проучване е подходящ или не. В случай че грешката на маржа е твърде голяма, може да се окаже, че размерът на извадката ни е твърде малък и трябва да го увеличим, така че резултатите от извадката да съвпадат по-тясно с резултатите от популацията.
Има някои сценарии, при които границата на грешката няма да бъде от голяма полза и няма да ни помогне да проследим грешката:
- Ако въпросите от анкетата не са проектирани и не помагат в получаването на необходимия отговор
- Ако хората, които отговарят на анкетата, имат някои пристрастия по отношение на продукта, за който се прави проучването, тогава също резултатът не е много точен
- Ако избраната извадка е подходящият представител на популацията, и в този случай резултатите ще бъдат изключени.
Също така, едно голямо предположение тук е, че населението е нормално разпределено. Така че, ако размерът на извадката е твърде малък и разпределението на популацията не е нормално, z резултатът не може да бъде изчислен и няма да можем да намерим границата на грешката.
Уместност и използване на маржа на формулата за грешка
Всеки път, когато използваме примерни данни, за да намерим някакъв подходящ отговор за съвкупността от популация, има известна несигурност и вероятност резултатът да се отклони от реалния резултат. Погрешността ще ни каже, че това, което е нивото на отклонение, е извадката от извадката. Трябва да сведем до минимум допустимата грешка, така че нашите примерни резултати да изобразяват действителната история на данните за населението. Така че по-ниска степен на грешка, по-добри ще бъдат резултатите. Пропускът на грешка допълва и допълва статистическата информация, която имаме. Например, ако проучване установи, че 48% от хората предпочитат да прекарват времето си вкъщи през уикенда, ние не можем да бъдем толкова точни и има някои липсващи елементи в тази информация. Когато тук въведохме допустима грешка, да речем, 5%, тогава резултатът ще се тълкува като 43-53% хора харесаха идеята да бъдат у дома през уикенда, което има пълен смисъл.
Калкулатор на формула за грешка
Можете да използвате следния марж на грешка калкулатор
| Z | |
| С | |
| √n | |
| Погрешка | |
| Погрешка | = |
|
|
Препоръчителни статии
Това е ръководство за формулата на маржа на грешката. Тук обсъждаме как да изчислим маржа на грешката заедно с практически примери. Предоставяме и калкулатор Margin of Error с изтеглящ се шаблон за excel. Можете също да разгледате следните статии, за да научите повече -
- Ръководство за формула на амортизация на права линия
- Примери на формула за удвояване на времето
- Как да изчислим амортизацията?
- Формула за централна гранична теорема
- Altman Z Score | Определение | Примери
- Формула за амортизация | Примери с шаблон на Excel