
Въведение в графиката в структурата на данните
Графиките са нелинейни структури от данни, съдържащи ограничен набор от възли и ръбове. Възлите са елементите, а ръбовете са подредени двойки връзки между възлите.
Забележете думата нелинейна. Нелинейната структура на данните е тази, при която елементите не са подредени в последователен ред. Например масивът е линейна структура на данни, защото елементите са подредени един след друг. Можете да преминете всички елементи на масив в един цикъл. Такъв не е случаят с нелинейните структури от данни. Елементите на нелинейната структура на данните са подредени на много нива, често следвайки йерархичен модел. Графиките са нелинейни.
Следващата дума, на която трябва да обърнете внимание, е ограничена. Дефинираме графиката, за да има краен и счетлив брой възли. Това е доста несъгласен термин. По същество Графика може да има безкраен брой възли и все още да е ограничена. Например родословно дърво, вариращо от Адам и Ева. Това е сравнително безкрайна графика, но все още е счетливо и затова се счита за крайна.
Пример в реалния свят
Най-добрият пример за графики в реалния свят е Facebook. Всеки човек във Facebook е възел и е свързан чрез ръбове. A е приятел на B. B е приятел на C и т.н.
терминология
Ето споменатите по-долу терминологии на графиката в структурата на данните
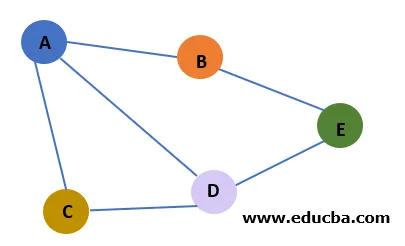
1. Представяне на графика: Като цяло графика е представена като двойка множества (V, E). V е съвкупността от върхове или възли. E е съвкупността от Edges. В горния пример,
V = (A, B, C, D, E)
E = (AB, AC, AD, BE, CD, DE)
2. Възел или връх: Елементите на графика са свързани чрез ръбове.
3. Краища: Път или линия между два върха в графика.
4. Съседни възли: Два възела се наричат съседни, ако са свързани през ръб. В горния пример възел A е в съседство с възлите B, C и D, но не и към възел E.
5. Path: Path е последователност от ръбове между два възла. Това е по същество траверса, започваща от един възел и завършваща на друга. В горния пример има множество пътища от възел A до възел E.
Път (A, E) = (AB, BE)
ИЛИ
Път (A, E) = (AC, CD, DE)
ИЛИ
Път (A, E) = (AD, DE)
6. Ненасочена графика: Ненасочена графика е тази, при която краищата не определят определена посока. Краищата са двупосочни.
пример
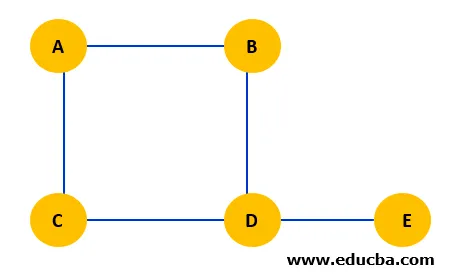
По този начин, в този пример, ръбът AC може да се премине от А до С и С до А. Подобно на всички ръбове. Път от възел В до възел С ще бъде (BA, AC) или (BD, DC).
7. Насочена графика: насочена графика е тази, при която краищата могат да се преминават само в определена посока.
пример
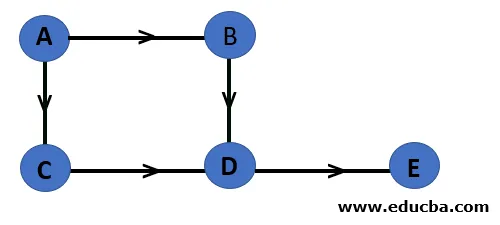
Така в същия пример сега ръбовете са насочени. Можете да преминете само по ръба по неговата посока. Вече няма път от възел B до възел C.
8. Претеглена графика: Графиката на претеглените е графика, където краищата са свързани с тежест. Това обикновено е цената за преминаване на ръба.
пример
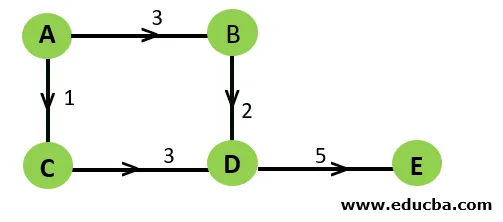
Така в същия пример, сега ръбовете имат определена тежест, свързана с тях. Има два възможни пътя между възел А до възел Е.
Path1 = (AB, BD, DE), тегло1 = 3 + 2 + 5 = 10
Path2 = (AC, CD, DE), тегло2 = 1 + 3 + 5 = 9
Ясно е, че човек би предпочел Path2, ако целта е да се достигне възел E от възел A с минимални разходи.
Основни операции на графика
Ето основните операции на графиката, споменати по-долу
1. Добавяне / премахване на Vertex
Това е най-простата операция в графиката. Просто добавяте върха към графика. Не е необходимо да се свързва с друг връх чрез ръб. Когато премахвате върха, трябва да премахнете всички ръбове, които произхождат от и завършват в изтрития връх.
2. Добавяне / премахване на ръба
Тази операция добавя или премахва ръб между два върха. Когато всички краища, произхождащи от и завършващи на върха, се изтриват, върхът се превръща в изолирана върха.
3. Първо търсене на ширина (BFS)
Това е траверсна операция в графиката. BFS хоризонтално пресича графиката. Това означава, че той преминава през всички възли на едно ниво, преди да премине към следващото ниво.
Алгоритъмът BFS започва в горната част на първия възел в графиката и след това преминава през всички съседни възли към него. След преминаване на всички съседни възли алгоритъмът повтаря една и съща процедура за дочерните възли.
пример
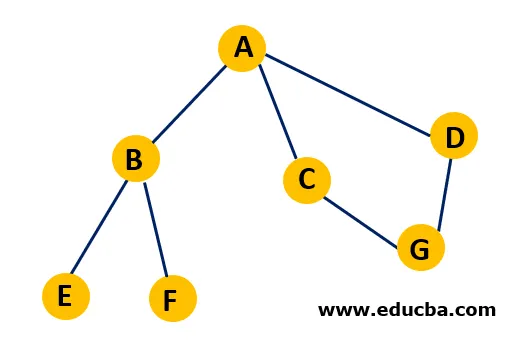
Преминаването на горната графика по BFS начин би се получило от A -> B -> C -> D -> E -> F -> G. Алгоритъмът започва от възел A и преминава през всички негови съседни възли B, C и D. Той маркира и четирите възли като посетени. След преминаване на всички съседни възли на А алгоритъмът се придвижва към първия съседен възел на А и повтаря същата процедура. В този случай възелът е B, а прилежащите възли към B са E и F. След това съседните възли към C се преминават. След като се посетят всички възли, операцията приключва.
4. Дълбоко първо търсене (DFS)
Дълбоко първо търсене или DFS обикаля вертикално графиката. Започва с коренния възел или първия възел на графиката и преминава през всички дъщерни възли, преди да се придвижи към съседните възли.
пример
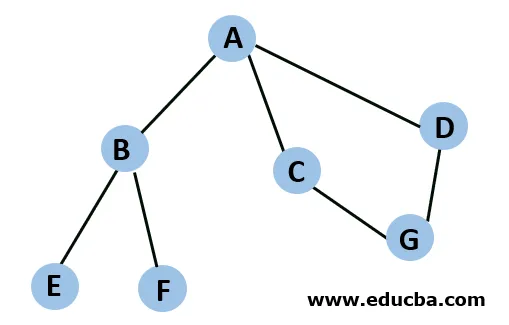
Преминаването на горната графика по BFS начин ще произтича от A -> B -> E -> F -> C -> G -> D. Алгоритъмът започва от възел A и преминава през всички негови дъщерни възли. Веднага щом се сблъска с B, изглежда, че има допълнителни детски възли. И така, дъщерните възли на B се преминават, преди да се премине към следващия долен възел на А.
Реално изпълнение на графиките
- Проектиране на електрически вериги за предаване на енергия.
- Проектиране на мрежа от взаимосвързани компютри.
- Проучване на молекулната, химическата и клетъчната структура на всяко вещество, например човешка ДНК.
- Проектиране на транспортни маршрути между градовете и местата в града.
Заключение - Графика в структурата на данните
Графиките са много полезна концепция в структурите на данните. Той има практически реализации в почти всяка област. Много е важно да се разберат основите на теорията на графите, да се разбере разбирането на алгоритмите на структурата на графиката.
Тази статия беше просто въведение в графиките. Това е просто стъпало. Препоръчително е да се гмуркате допълнително в темата за теорията на графиките.
Препоръчителни статии
Това е ръководство за графиката в структурата на данните. Тук обсъждаме терминологиите и основните операции на графиката в структурата на данните. Можете също да разгледате следната статия, за да научите повече -
- Въпроси за интервю за структурата на данните
- Модел на данни в Касандра
- Какво е Data Mart?
- Какво е Data Scientist?