
Формула за F-тест (Съдържание)
- формула
- Примери
Какво е F-Test Formula?
F-тестът е статистически тест, който ни помага да открием дали две групи от популации, които имат нормално разпределение на своите точки от данни, имат еднакво стандартно отклонение или отклонения. Но първото и основно нещо за извършване на F-тест е, че наборите от данни трябва да имат нормално разпределение. Това се прилага за разпределение на F при нулевата хипотеза. F-тестът е много важна част от Анализа на вариацията (ANOVA) и се изчислява, като се вземат съотношения на две вариации на два различни масива данни. Както знаем, че отклоненията ни дават информация за разпръскването на точките от данни. F-тестът се използва и в различни тестове като регресионен анализ, тест Чоу и т.н.
Формула за F-тест:
Няма проста формула за F-Test, но това е поредица от стъпки, които трябва да следваме:
Стъпка 1: За да извършим F-тест, първо трябва да определим нулевата хипотеза и алтернативната хипотеза. Те се дават от: -
- H0 (нулева хипотеза): Вариант на 1- ви набор от данни = Variance на 2- ри набор от данни
- Ha: Вариант на 1- ви набор от данни <Вариант на втория набор от данни (за долен тест с едно опашка)
- Ha: Вариант на 1- ви набор от данни> Вариант на 2- ри набор от данни (за горен тест с едно опашка)
- Ha: Вариант на 1- ви набор от данни ≠ Вариант на 2- ри набор от данни (за двустранен тест)
Стъпка 2: Следващото нещо, което трябва да направим е, че трябва да открием нивото на значимост и след това да определим степените на свобода както на числителя, така и на знаменателя. Това ни помага да определим техните критични стойности. Степен на свобода е размер на извадката -1.
Стъпка 3: Формула на F-тест:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Стъпка 4: Намерете F критичната стойност от таблицата F, като вземете степен на свобода и ниво на значимост.
Стъпка 5: Сравнете тези две стойности и ако критичната стойност е по-малка от стойността F, можете да отхвърлите нулевата хипотеза.
Примери за формула на F-тест (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на F-Test.
Можете да изтеглите този шаблон на F-TEST формула Excel тук - шаблон на F-TEST формула ExcelФормула за F-тест - Пример №1
Да приемем, че имаме два набора от данни A&B, които съдържат различни точки от данни. Извършете F-тест, за да определим дали можем да отхвърлим нулевата хипотеза при ниво на значимост 1%.
Набори от данни:
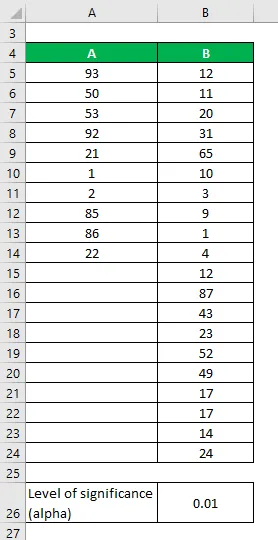
Решение:
Нулева хипотеза: Вариант на A = вариант на B
Степен на свобода се изчислява като
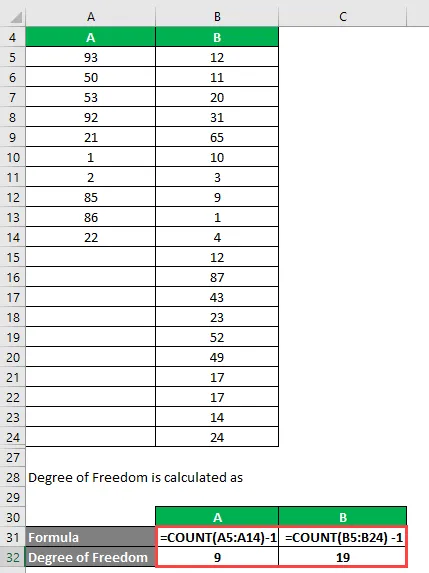
Степен на свобода
- За A = 10 - 1 = 9
- За B = 20 - 1 = 19
Вариантът се изчислява като:

- Вариант на A = 1385.61
- Вариант на B = 521.22
F Стойността се изчислява по формулата, дадена по-долу
F Стойност = Вариант на 1- вия набор от данни / Вариант на 2- ри набор от данни
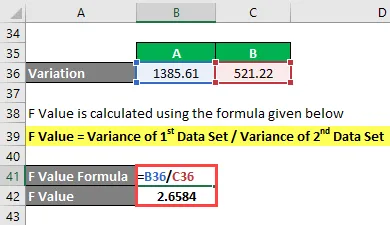
- F стойност = 1385, 61 / 521, 22
- F стойност = 2.6584
F-таблица:
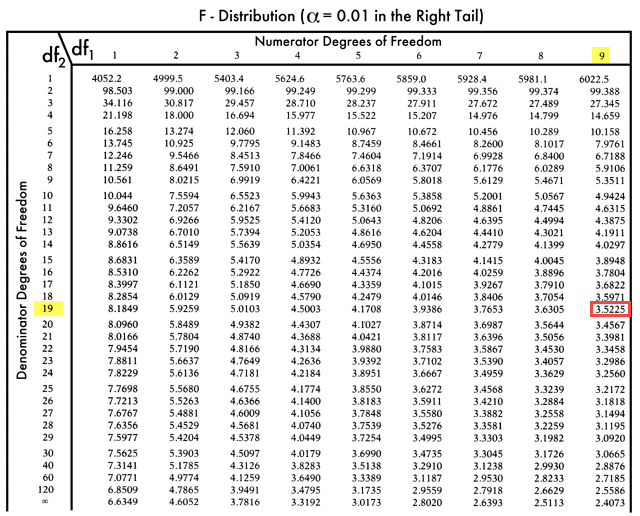
Значи F критична стойност = 3, 5225
Тъй като F критичната е по-голяма от стойността на F, не можем да отхвърлим нулевата хипотеза.
Формула за F-тест - Пример №2
Да предположим, че работите в изследователска компания и искате нивото на емисиите на въглероден оксид да се случи от две различни марки цигари и дали те са значително различни или не. В своя анализ сте събрали следната информация:
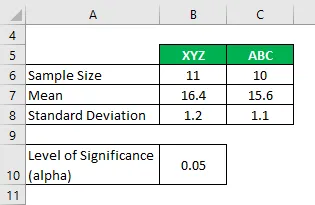
Решение:
Степен на свобода се изчислява като
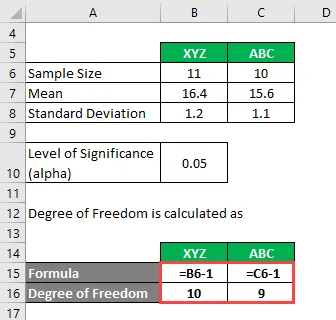
Степен на свобода
- За XYZ = 11 - 1 = 10
- За ABC = 10 - 1 = 9
Вариантът се изчислява като:
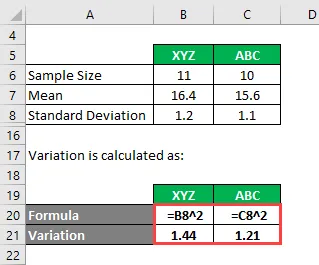
- Вариант на XYZ = 1, 2 2 = 1, 44
- Вариант на ABC = 1.1 2 = 1.21
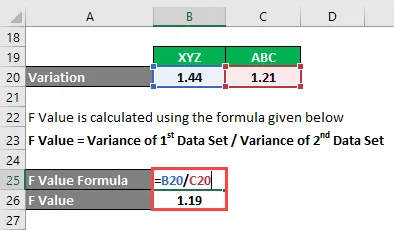
- F стойност = 1, 44 / 1, 21
- F стойност = 1, 19
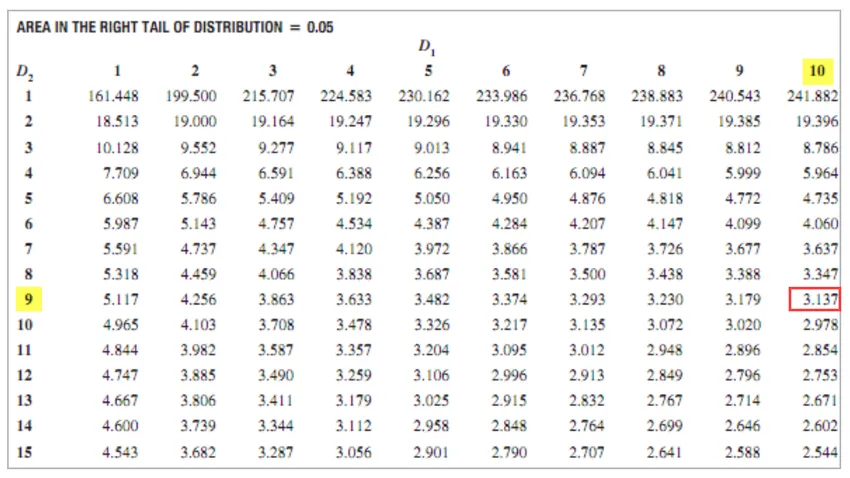
F Критична стойност = 3.137
Тъй като F критичната> F стойност, нулевата хипотеза не може да бъде отхвърлена.
обяснение
В горните примери видяхме приложението на F-Test и как се изпълнява. Но има набор от предположения, за които трябва да се погрижим преди да извършим F-Test, в противен случай няма да получим необходимите резултати:
- Първото нещо е, че винаги трябва да поставяме числителя на по-високата стойност на дисперсията, докато изчисляваме F стойността. Така че, ако F = V1 / V2, V1 трябва да бъде> V2
- Ако искаме да извършим 2 теста на опашката, трябва да разделим нивото на значимост на 2 и това ще е правилното ниво, за да намерим критичната стойност
- Използваме само дисперсия е изчислението на стойността F и ако сме дадени със стандартни отклонения, както в пример 2, те трябва да бъдат квадратни, за да намерят отклонението.
- И двете проби трябва да са независими една от друга, а размерът на пробата да бъде по-малък от 30
- Популационните групи, от които са взети пробите, трябва да бъдат нормално разпределени
Това са ключовите параметри / предположение, за които трябва да се внимава при изпълнение на F-Test.
Уместност и използване на формулата за F-тест
F-Test, както беше обсъдено по-горе, ни помага да проверим за равенството на двете вариации на популацията. Така че, когато имаме две независими проби, които са взети от нормална популация и искаме да проверим дали имат една и съща променливост, използваме F-тест. F-тестът също има голямо значение в регресионния анализ, а също и за тестване на значимостта на R2. Накратко, F-Test е много важен инструмент в статистиката, ако искаме да сравним вариацията на 2 или повече набора от данни. Но трябва да имате предвид всички предположения, преди да извършите този тест.
Препоръчителни статии
Това е ръководство за формулата на F-Test. Тук обсъждаме как да изчислим F-Test заедно с практически примери и изтеглящ се шаблон на excel. Можете също да разгледате следните статии, за да научите повече -
- Формула за разпределение
- Формула за ценообразуване на облигации
- Формула за грешка в проценти
- Изчисляване на формула на NOPAT