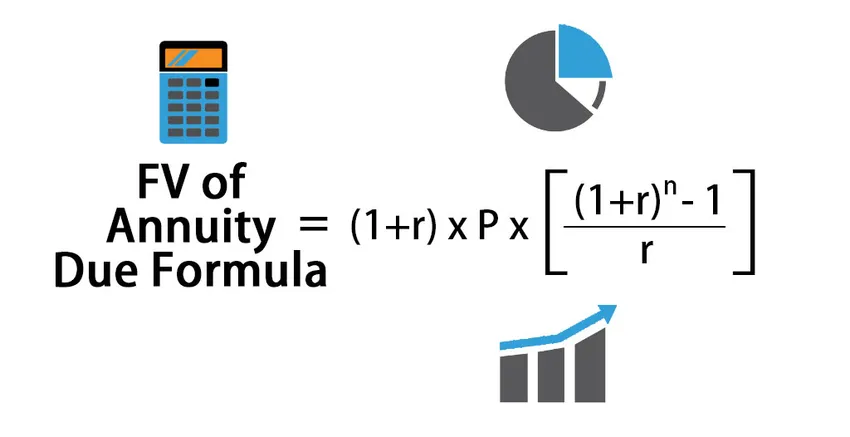
Бъдеща стойност на формулата за дължима ануитетност (Съдържание)
- Бъдеща стойност на формулата за дължимост на анюитет
- Примери за бъдеща стойност на формула за дължима ануитетност (с шаблон на Excel)
- Калкулатор на формула за бъдеща стойност на дължимата формула на ануитет
Бъдеща стойност на формулата за дължимост на анюитет
Формулата за изчисляване на бъдещата стойност на дължимата анюитет:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Където,
- P = Периодично плащане
- R = процент за период
- N = брой на периодите
Примери за бъдеща стойност на формула за дължима ануитетност (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на бъдещата стойност на дължимата ануитетност.
Можете да изтеглите този шаблон за бъдеща стойност на формула за Excel Формула Excel тук - Бъдеща стойност на формула ExcelПример №1
Да предположим, че Ананд е депозирал 10 000 долара годишно, а ефективната ставка, която му предлага сметката, е 3%. Сега Ананд иска да изчисли бъдещия си баланс след 5 години, като поема първия депозит от днес нататък.
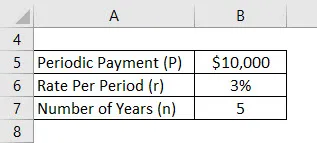
Решение:
Бъдещата стойност на дължимата анюитет се изчислява по формулата, дадена по-долу
FV на дължимата ануитетна стойност = (1 + r) * P * (((1 + r) n - 1) / r)
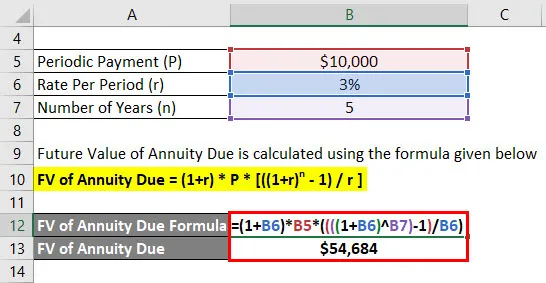
- FV на ануитетна дължина = (1+ 3%) * $ 10 000 * (((((1 + 3%) 5) - 1) / 3%)
- FV на ануитетната дължина = $ 54 684
След 5 години Ананд ще получи бъдещо салдо на 54 684 долара.
Пример №2
Да предположим, че Jagriti е депозирал 8000 долара годишно, а ефективната ставка, която му предлага сметката, е 5%. Сега Джагрити иска да изчисли бъдещия си баланс след 5 години с поемането на първи депозит от днес нататък.

Решение:
Бъдещата стойност на дължимата анюитет се изчислява по формулата, дадена по-долу
FV на дължимата ануитетна стойност = (1 + r) * P * (((1 + r) n - 1) / r)
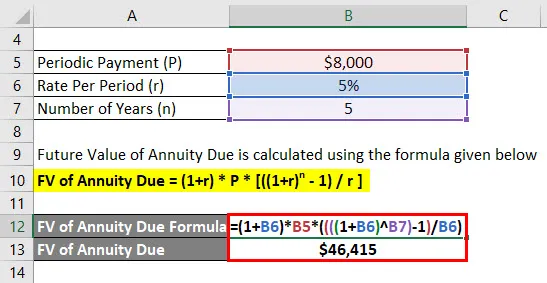
- FV на дължимата ануитетна стойност = (1+ 5%) * $ 8 000 * (((((1 + 5%) 5) - 1) / 5%)
- FV на ануитетната дължина = 46 415 долара
Джагрити ще получи бъдещо салдо в размер на 46 415 долара след 5 години.
Пример №3
Да предположим, че Anandriti е депозирал 20 000 долара годишно, а ефективната ставка, която му предлага сметката, е 2%. Сега Анандрити иска да изчисли бъдещия си баланс след 5 години, като поема първия депозит от днес нататък.
Решение:
Бъдещата стойност на дължимата анюитет се изчислява по формулата, дадена по-долу
FV на дължимата ануитетна стойност = (1 + r) * P * (((1 + r) n - 1) / r)
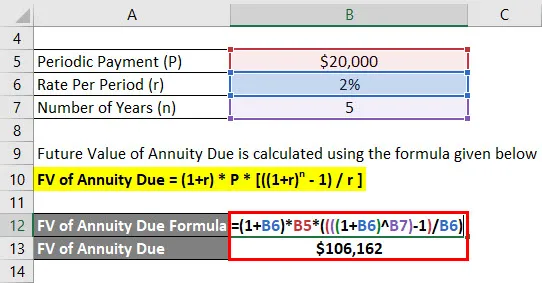
- FV на дължимата ануитетна стойност = (1+ 2%) * $ 20 000 * (((((1 + 2%) 5) - 1) / 2%)
- FV на дължимата сума за ануитет = 1, 06, 162 долара
След 5 години Anandriti ще получи бъдещо салдо в размер на 1, 06, 162 долара.
обяснение
За да изчислим крайната стойност за поредица от парични потоци или плащания, при които първата вноска се получава незабавно, използваме бъдещата стойност на дължимата рента. Първата моментална вноска или плащане разграничават анюитета поради обикновения анюитет. Непосредственият или моментален анюитет се нарича дължима анюитет.
Той изчислява стойността на паричните потоци в бъдещ период. Използването на дължимата FV на рентата в реални ситуации е различна от настоящата стойност на дължимата рента. Да предположим, например, че фирма или физическо лице купуват рента и са платили първата вноска днес. Можем да използваме примера, за да обясним допълнително, да предположим, че компания или физическо лице искат да купят анюитет от всеки и са извършили първото плащане днес. За да изчислим цената, която трябва да платим в тази ситуация, можем да използваме настоящата стойност на формулата за дължима рента. Ако обаче искаме да изчислим оставащото салдо след спестяване на лихвата за 5 години в сметката и решихме да изплатим първата вноска днес, в този случай се използва бъдещата стойност на анюитет. Дължимата рента може да се обясни като вид анюитет, при който паричните потоци възникват в началото на всеки период. Поради усъвършенствания характер на паричните потоци, всеки паричен поток е подложен на ефекта на усложняване за всеки допълнителен период, в случай че се сравнява с обикновена рента. Бъдещата стойност на обикновения анюитет е по-ниска от бъдещата стойност на анюитета, тъй като бъдещата стойност на анюитета получава периодична лихва от коефициента на един плюс.
Уместност и използване на бъдещата стойност на дължимата анюитет
Нека да разберем значението на бъдещата стойност и анюитет, дължими отделно. Бъдещата стойност може да се обясни като общата стойност за парична сума, която трябва да бъде изплатена в бъдеще на определена дата. А дължимата рента може да се обясни като поредицата от плащания, които се извършват в началото на всеки период в редовна последователност. Следователно бъдещата стойност на дължимия анюитет може да се обясни като общата стойност на определена бъдеща дата за поредица от системни / периодични плащания, когато плащанията се извършват в началото на всеки период. Този вид транзакция и такъв поток от плащания могат да се видят за сметка на получателя на пенсионния план. Общата стойност е сумата, до която ще нараснат поредицата от плащания, извършени в бъдещата дата, тъй като се приема определен размер на лихвата, а печалбите постепенно се увеличават за определен период. Изчисляването на бъдещата стойност на обикновен анюитет е идентично с това, но единствената разлика е, че добавяме допълнителен период на плащане, който се прави в началото.
Калкулатор на формула за бъдеща стойност на дължимата формула на ануитет
Можете да използвате следния калкулатор на бъдещата стойност на анюитетния калкулатор
| P | |
| R | |
| н | |
| Бъдеща стойност на формулата за дължимост на анюитет | |
| Формула за бъдеща стойност на дължимата формула за анюитет = | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Препоръчителни статии
Това е ръководство за Формула за бъдеща стойност на анюитетна дължима формула. Тук обсъждаме как да изчислим бъдещата стойност на дължимия анюитет заедно с практически примери. Ние също така предлагаме калкулатор на бъдещата стойност на анюитет, с изтеглящ се шаблон Excel. Можете също да разгледате следните статии, за да научите повече -
- Ръководство за формула на стойността на парите във времето
- Примери за формула на сегашния фактор на стойността
- Калкулатор за формула на информационното съотношение
- Формула за степен на оперативен ливъридж