
Коефициент на формула за определяне (Съдържание)
- формула
- Примери
Какъв е коефициентът на формула за определяне?
В статистиката коефициентът на определяне, наричан още R2, е инструмент, който определя и оценява способността на статистически модел да обяснява и прогнозира бъдещи резултати. С други думи, ако имаме зависима променлива у и независима променлива х в модела, тогава R2 помага при определянето на изменението в y чрез вариант x. Той е един от основните резултати от регресионния анализ и се използва, когато искаме да прогнозираме бъдеще или да тестваме някои модели със свързана информация. Стойността на R2 е между 0 и 1 и по-висока стойност на R 2, по-добре ще бъде прогнозирането и силата на модела. R2 е много подобен на коефициента на корелация, тъй като коефициентът на корелация измерва пряката връзка на две променливи. R 2 е основно квадрат на коефициент на корелация.
Формула за коефициент на определяне:
Има няколко формули за изчисляване на коефициента на определяне:
- Използване на Коефициент на корелация:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Където:
- X - Точки от данни в набор данни X
- Y - Точки от данни в набор данни Y
- X m - Средно на набор от данни X
- Y m - Средна стойност на набора данни Y
Така
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Използване на регресионни изходи
Коефициент на определяне (R 2 ) = обяснено изменение / общо изменение
Коефициент на определяне (R 2 ) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Където:
- TSS - Обща сума от квадрати = Σ (Yi - Ym) 2
- MSS - Моделна сума от квадрати = Σ (Y - Ym) 2
- RSS - остатъчна сума от квадрати = Σ (Yi - Y ^) 2
Y е прогнозираната стойност на модела, Yi е i-тата стойност и Ym е средната стойност
Примери за коефициент на формула за определяне (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на коефициента на определяне.
Можете да изтеглите този Коефициент на формула за формулиране на формула Excel тук - Коефициент на формула за формулировка Excel шаблонКоефициент на формула за определяне - пример №1
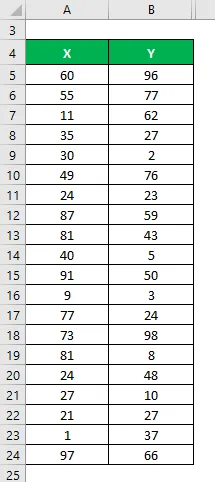
Да речем, че имаме два набора данни X&Y и всеки съдържа 20 произволни точки от данни. Изчислете коефициента на определяне за набора данни X&Y.
Средната стойност се изчислява като:
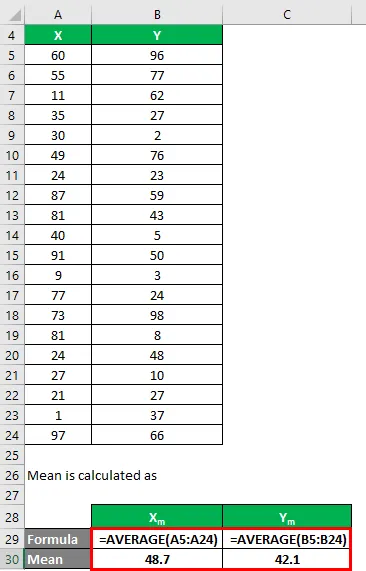
- Средно на набор от данни X = 48.7
- Средно на набор от данни Y = 42.1
Сега трябва да изчислим разликата между точките от данни и средната стойност.
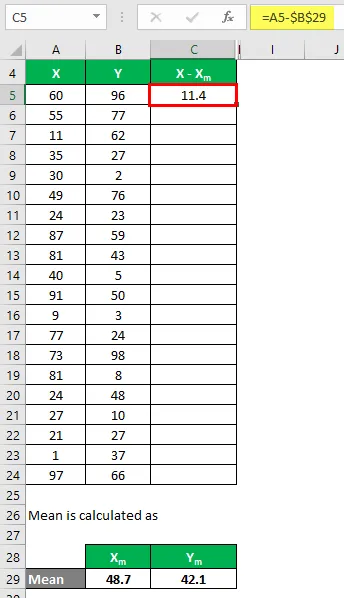
По същия начин, изчислете за всички набори от данни на X.
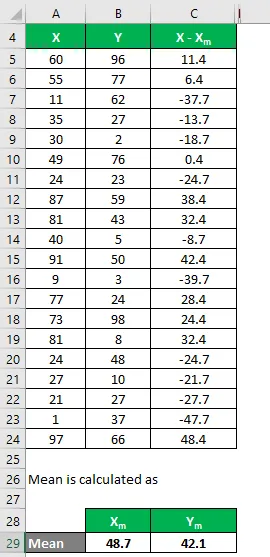
По същия начин, изчислете го и за набор от данни Y.

Изчислете квадрата на разликата за двата набора от данни X и Y.
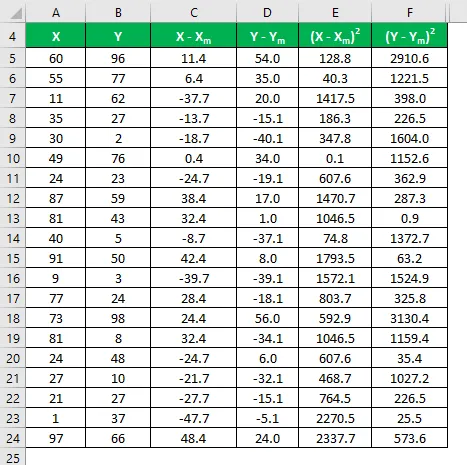
Умножете разликата в X с Y.
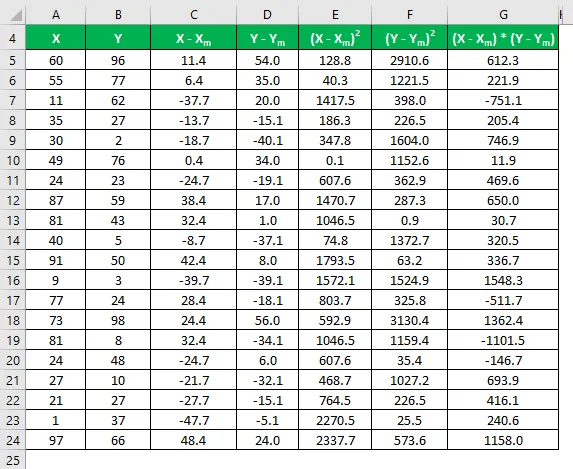
Коефициентът на корелация се изчислява по формулата, дадена по-долу
Коефициент на корелация = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
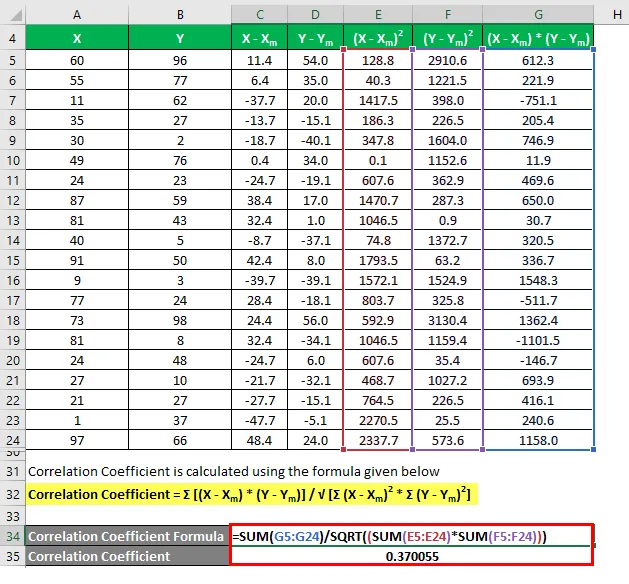
Коефициентът на определяне се изчислява по формулата, дадена по-долу
Коефициент на определяне = (Коефициент на корелация) 2
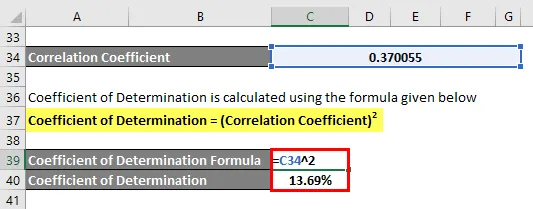
Коефициент на определяне = 13, 69%
Коефициент на формула за определяне - пример №2
Нека да кажем, че сте много рискован инвеститор и искате да инвестирате пари на фондовия пазар. Не сте сигурни в кои акции да инвестирате, а също и рискът ви апетит е нисък. Така че искате да инвестирате в акции, които са безопасни и могат да имитират представянето на индекса. Вашият приятел, който е активен инвеститор, включи в списъка си 3 акции за вас въз основа на тяхната основна и техническа информация и искате да изберете 2 акции сред тези три.
Вие също сте събрали информация за техните исторически доходи за последните 15 години.
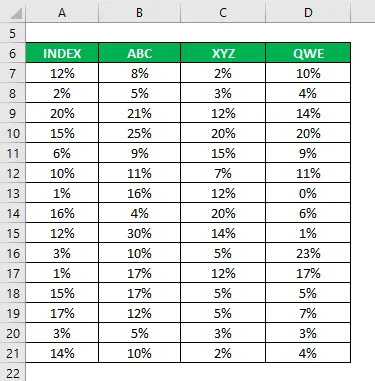
Коефициентът на корелация се изчислява по формулата на excel
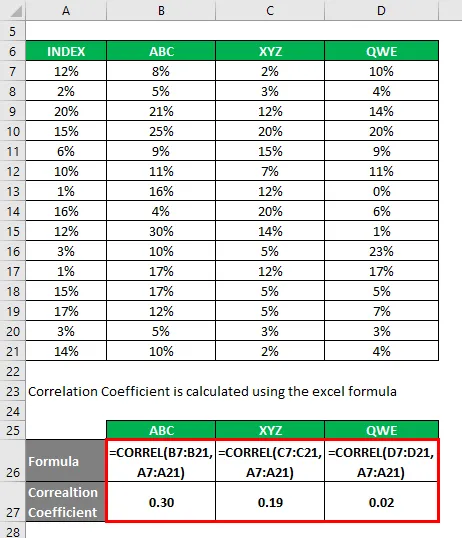
Коефициентът на определяне се изчислява по формулата, дадена по-долу
Коефициент на определяне = (Коефициент на корелация) 2
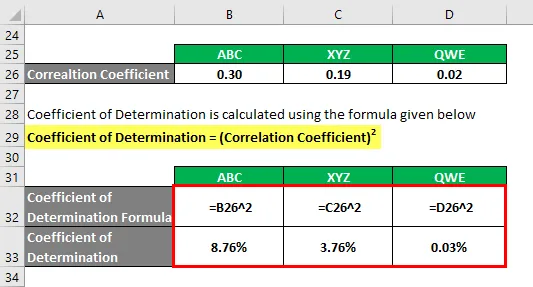
Въз основа на информацията ще изберете акции ABC и XYZ за инвестиране, тъй като те имат най-висок коефициент на определяне.
обяснение
Коефициентът на определяне, както е обяснено по-горе, е квадратът на корелацията между два набора от данни. Ако R2 е 0, това означава, че няма корелация и независима променлива не може да предвиди стойността на зависимата променлива. По същия начин, ако стойността му е 1, това означава, че независимата променлива винаги ще бъде успешна при прогнозиране на зависимата променлива. Но има и някои ограничения. Въпреки че ни казва връзката между 2 набора от данни, тя не ни казва дали тази стойност е достатъчна или не.
Също така, голямата стойност R2 не винаги означава, че двете променливи имат силни връзки и това може да бъде грешка. Например: Да кажем, че стойността на R 2 между няколко коли, продадени за една година, и броя на кутиите за сладолед, продадени за една година, е 80%. Но няма връзка между тези две. Така че човек трябва да бъде много внимателен, докато използва R2 и първо да разбере данните и след това да приложи метода
Уместност и използване на коефициента на формула за определяне
Има много практически приложения на R 2 . Например, R2 много често се използва от инвеститорите, за да сравняват представянето на своя портфейл с пазара и да се опитват да прогнозират и бъдещи направления. По същия начин хедж фондовете използват R 2 им помага да моделират риска в своите модели. Но в крайна сметка резултатът се основава на чисти числа и статистически данни, които понякога могат да бъдат подвеждащи. Както бе споменато по-горе, първо трябва да се провери дали изходът на R 2 има смисъл в реалния живот или не.
Препоръчителни статии
Това е ръководство за Коефициент на формула за определяне. Тук обсъждаме как да изчислим коефициента на определяне, заедно с практически примери и свалящ се шаблон на excel. Можете също да разгледате следните статии, за да научите повече -
- Ръководство за Формула за рисков риск Premium
- Примери за формула на коефициента на покритие
- Калкулатор за формула на разходите, базирана на дейности
- Как да изчислим информационното съотношение с помощта на формула?