
Въведение във функциите в R
Функцията се дефинира като набор от оператори, за да изпълнява и изпълнява всяка конкретна логическа задача. Функцията приема някои входни параметри, които са известни като аргументи за изпълнение на тази задача. Функциите помагат за разбиването на кода, на по-прости парчета, като го организирате логически, което е по-лесно за четене и разбиране. В тази тема ще научим за функциите в R.
Как да напиша функции в R?
За да напишете функцията в R, ето синтаксиса:
Fun_name <- function (argument) (
Function body
)
Тук може да се види специфична запазена дума за функция, използвана в R, за да се дефинира всяка функция. Функцията приема вход, който е под формата на аргументи. Функционалното тяло е набор от логически оператори, които се изпълняват над аргументи и след това той връща изхода. „Fun_name“ е името, дадено на функцията, чрез което може да се извиква навсякъде в програмата R.
Нека да видим пример, който ще бъде по-разяснен в разбирането на концепцията за функцията в Р.
R код
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
изход:
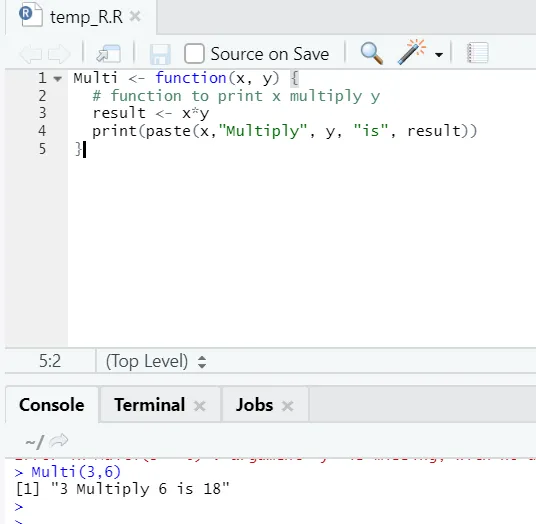
Тук създадохме името на функцията “Multi”, което приема два аргумента като входни данни и осигурява умноженият изход. Първият аргумент е x, а вторият аргумент е y. Както можете да видите, ние нарекохме функцията с името “Multi”. Тук, ако някой иска, аргументите също могат да бъдат зададени на стойността по подразбиране.
Различни видове функции в R
Различни R функции със синтаксис и примери (вградени, математически, статистически и т.н.)
1) Вградена функция -
Това са функциите, които идват с R за адресиране на конкретна задача, като вземат аргумент като вход и дават изход въз основа на дадения вход. Нека да обсъдим някои важни общи функции на R тук:
а) Сортиране: Данните могат да бъдат от сортиране във възходящ или низходящ ред. Данните могат да бъдат дали вектор на продължаваща променлива или факторна променлива.
Синтаксис:

Ето обяснението на неговите параметри:
- x: Това е вектор на непрекъснатата променлива или факторна променлива
- намаляващ: Това може да бъде зададено или True / False за контрол на реда чрез възходящ или низходящ. По подразбиране е FALSE`.
- последно: Ако векторът има стойности на NA, трябва ли да бъде поставен последен или не
R код и изход:
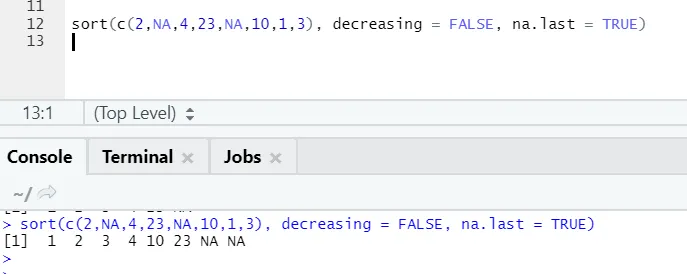
Тук можете да забележите как „NA“ стойностите се подравняват в края. Тъй като нашият параметър na.last = True беше вярно.
б) Seq: генерира последователност от числото между две определени числа.
Синтаксис
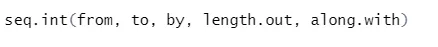
Ето обяснението на неговите параметри:
- от, за начална и крайна стойност на последователността.
- от: Увеличение / пролука между две последователни числа в последователност
- length.out: необходимата дължина на последователността.
- Along.with: Отнася се до дължината от дължината на този аргумент
R код и изход:
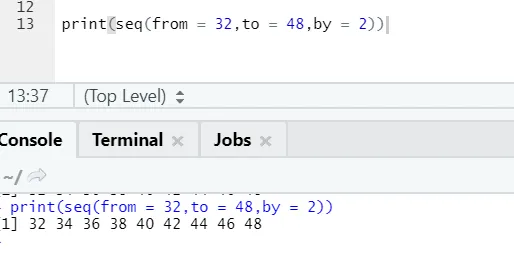
Тук може да се забележи, че генерираната последователност е с нарастване на 2, защото с е дефинирана като 2.
c) Toupper, tolower: Двете функции: toupper и tolower са функции, приложени върху низ, за да се променят случаите на буквите в изреченията.
R код и изход:
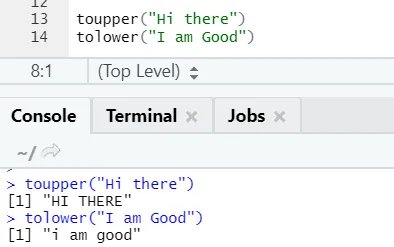
Човек може да забележи как случаите на буквите се променят, когато се прилагат към функцията.
г) Rnorm: Това е вградена функция, която генерира случайни числа.
R код и изход:
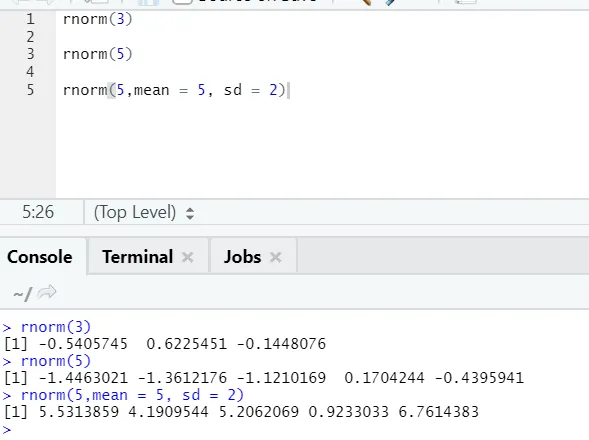
Функцията rnorm взема първия аргумент, който казва колко числа трябва да бъдат генерирани.
д) Rep: Тази функция възпроизвежда стойността толкова пъти, колкото е посочена.
R синтаксис: rnorm (x, n)
Тук х представлява стойност за репликация, а n представлява броя пъти, които трябва да бъдат повторени.
R код и изход:
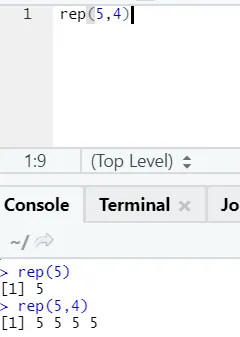
f) Поставяне: Тази функция е да обединява низове заедно с някакъв специфичен символ между тях.
синтаксис
paste(x, sep = “”, collapse = NULL)
R код
paste("fish", "water", sep=" - ")
R изход:
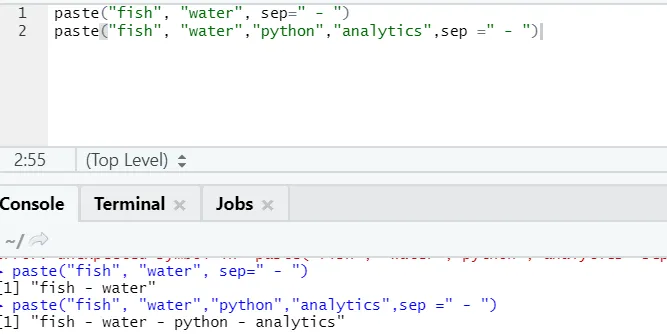
Както виждате, можем да залепим и повече от два низа. Sep е този специфичен характер, който добавихме между низовете. По подразбиране сеп е пространство.
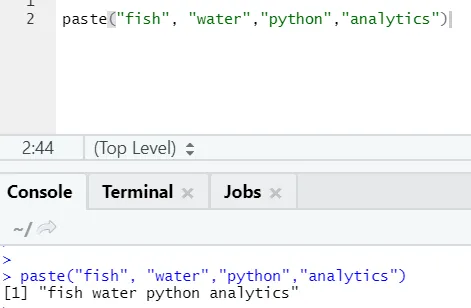
Има още една подобна функция като тази, която всички трябва да знаят, е pas0.
Функцията paste0 (x, y, колапс) работи подобно на паста (x, y, sep = “”, сгъване)
Моля, вижте примера по-долу:
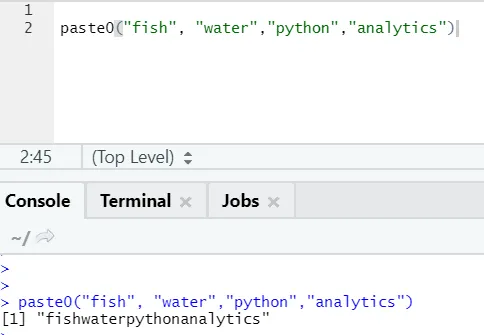
С прости думи, за да обобщим паста и паста0:
Paste0 е по-бърза от паста, когато става въпрос за свързване на низове без разделител. Тъй като пастата винаги търси „sep“ и което е място по подразбиране в нея.
ж) Strsplit: Тази функция е за разделяне на низа. Нека видим простите случаи:
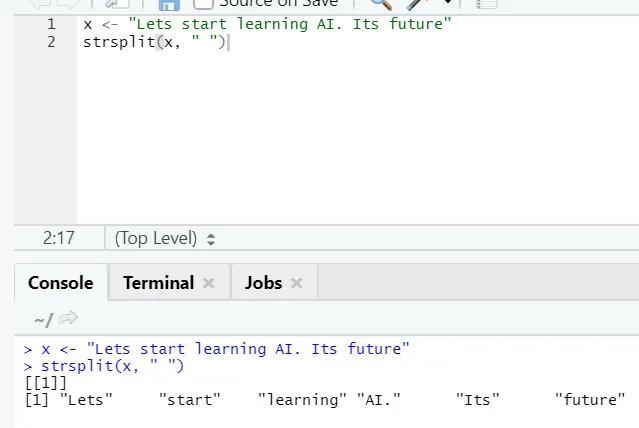
з) Rbind: Функцията rbind помага при комбиниране на вектори с еднакъв брой колони, една над друга.
пример
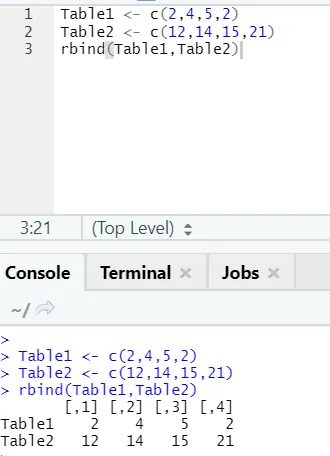
i) cbind: Това комбинира векторите със същия брой редове, един до друг.
пример
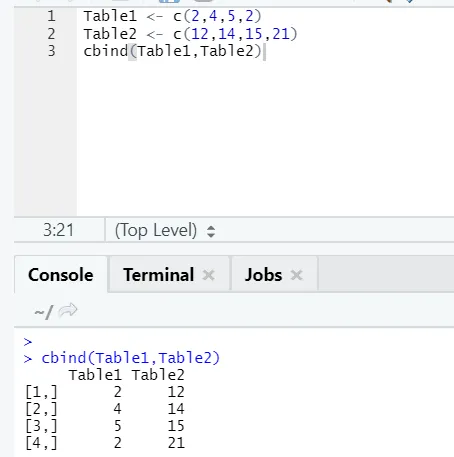
В случай, че броят на редовете не съвпада, по-долу е грешката, която ще намерите:

И двете cbind и rbind помагат при манипулиране и преформулиране на данни.
2) Математическа функция -
R осигурява голямо разнообразие от математически функции. Нека да видим няколко от тях подробно:
a) Sqrt: Тази функция изчислява квадратния корен на число или числов вектор.
R код и изход:
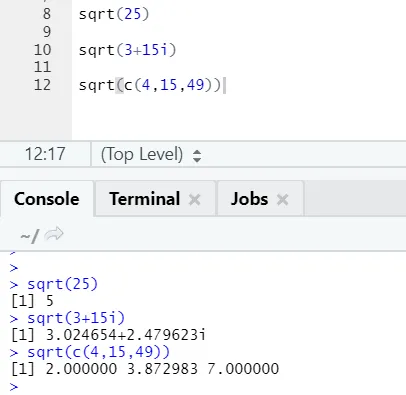
Може да се види как се изчислява корен на число, комплексно число и последователност от числов вектор.
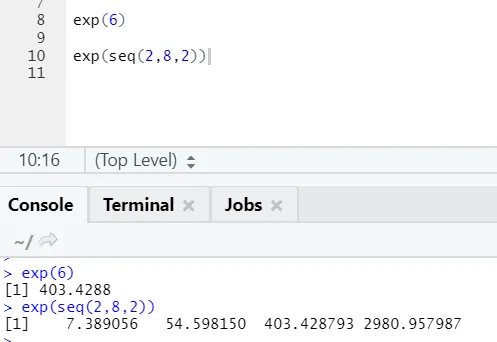
б) Exp: Тази функция изчислява експоненциалната стойност на число или числов вектор.
R код и изход:
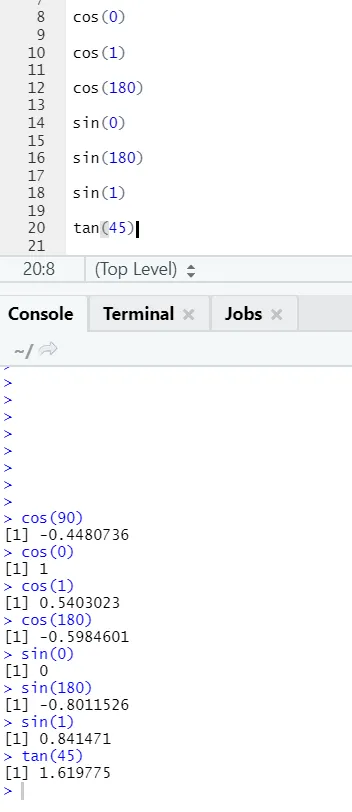
в) Cos, Sin, Tan: Това са тригонометрични функции, реализирани в R тук.
R код и изход:
г) Abs: Тази функция връща абсолютната положителна стойност на число.
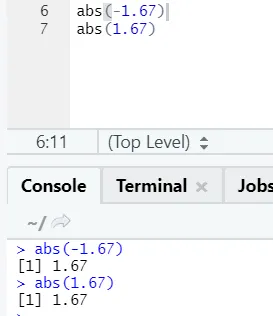
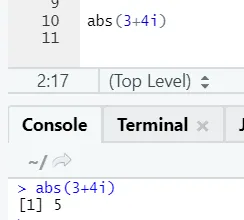
Както можете да видите, отрицателното или положителното на число ще бъде върнато в абсолютната си форма. Нека го видим за сложен номер:
д) Дневник: Това е, за да намерите логаритъм на число.
Ето примера е показан по-долу:
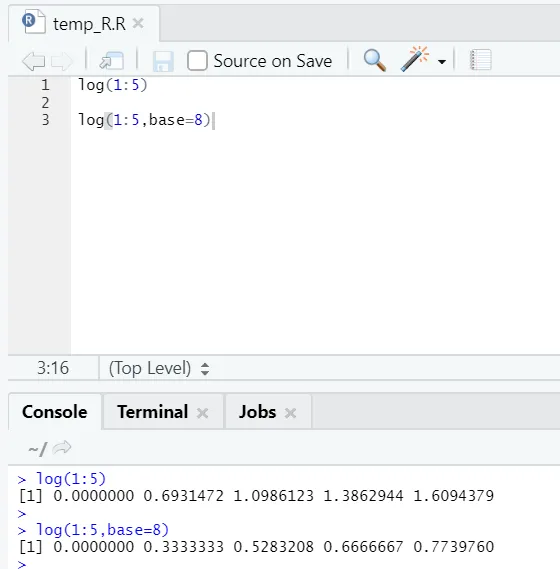
Тук човек получава гъвкавостта да променя основата според изискванията.
е) Cumsum: Това е математическа функция, която дава кумулативни суми. Ето примера по-долу:
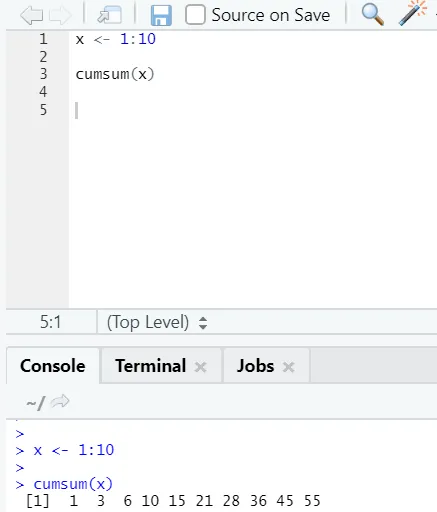
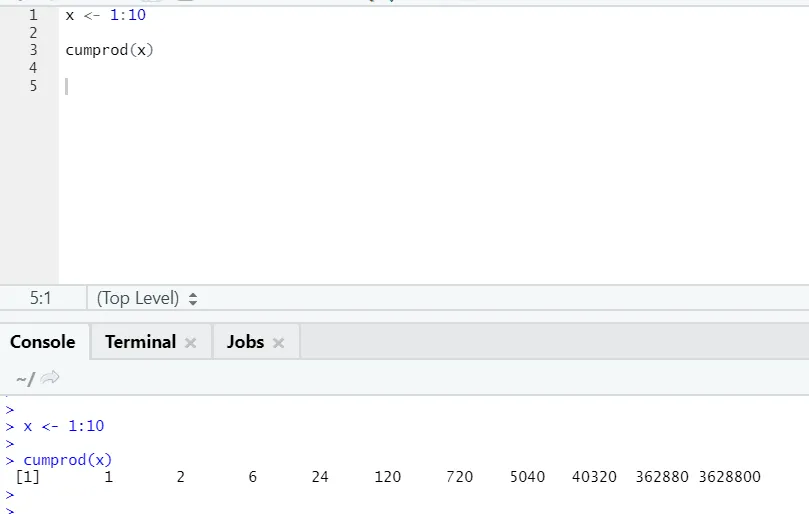
ж) Cumprod: Подобно на математическата функция на Cumsum, ние имаме cumprod там, където се случва кумулативно умножение.
Моля, вижте примера по-долу:
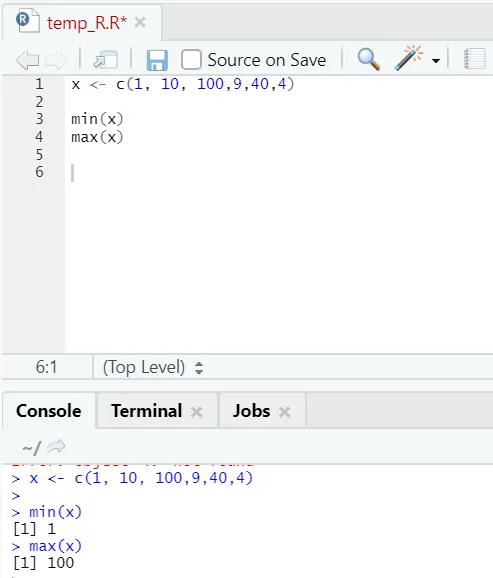
з) Макс, Мин: Това ще ви помогне да намерите максималната / минималната стойност в набора от числа. Вижте по-долу примерите, свързани с това:
i) Таван: Таванът е математическа функция връща най-малкото от цялото число по-високо от посоченото.
Нека разгледа пример:
таван (2.67)
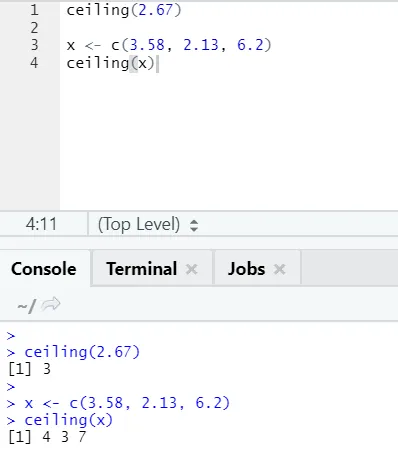
Както можете да забележите, таванът се прилага върху число, както и над списък, а получената продукция е най-малката от следващото по-високо цяло число.
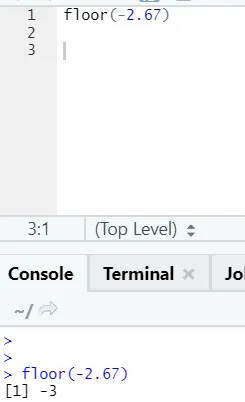
j) Етаж: Подът е математическа функция, връща най-малкото число на стойността от посоченото число.
Примерът, показан по-долу, ще ви помогне да го разберете по-добре:
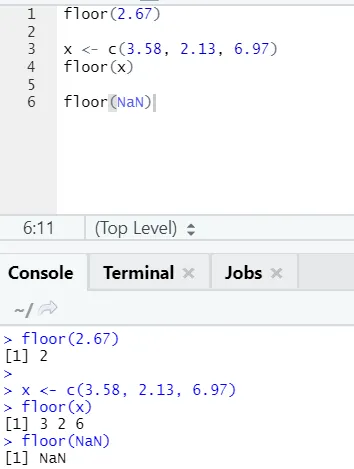
Той работи по същия начин и за отрицателни стойности. Моля, погледнете:
3) Статистически функции -
Това са функциите, които описват свързаното разпределение на вероятностите.
а) Медиана: Това изчислява медианата от последователността на числата.
Синтаксис
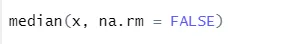
R код и изход:
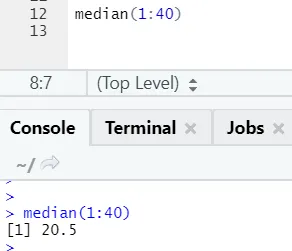
б) Днорма: Това се отнася до нормалното разпределение. Функцията dnorm връща стойността на функцията на плътността на вероятностите за нормалното разпределение, зададени параметри за x, μ и σ.
R код и изход:
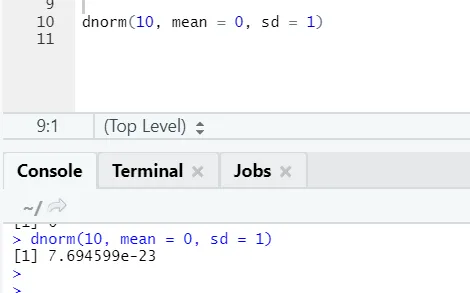
в) Cov: ковариацията казва дали два вектора са положително, отрицателно или напълно не са свързани.
R код
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
R изход:
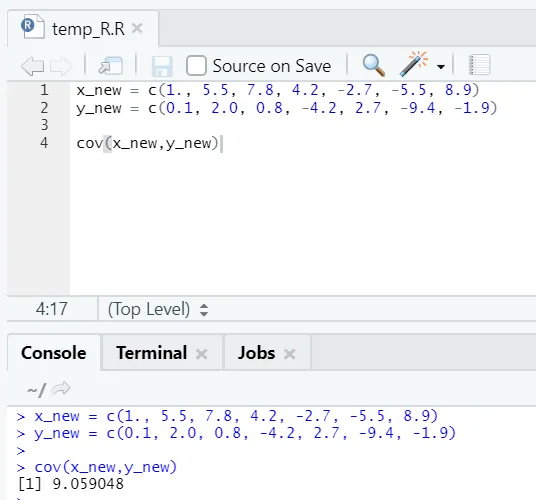
Както можете да видите, два вектора са положително свързани, което означава, че и двата вектора се движат в една и съща посока. Ако ковариацията е отрицателна, това означава, че x и y са обратно свързани и следователно се движи в обратна посока.
г) Кор: Това е функция за намиране на корелацията между векторите. Той всъщност дава коефициент на свързване между двата вектора, който е известен като „коефициент на корелация“. Корелацията добавя степен на коефициент спрямо ковариацията. Ако два вектора са положително свързани, корелацията също ще ви каже с колко разширяване са положително свързани.
Тези три типа методи, които могат да бъдат използвани за намиране на връзка между два вектора:
- Pearson корелация
- Кендал корелация
- Корелация на Spearman
В прост R формат изглежда така:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Тук x и y са вектори.
Нека да видим практическия пример за корелация на вграден набор от данни.
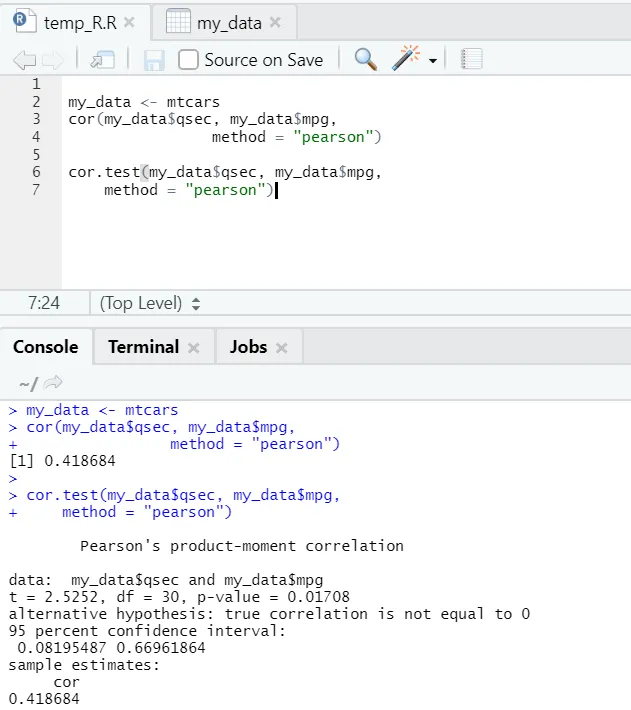
Така че тук можете да видите функцията „cor ()“ даде коефициента на корелация 0, 41 между „qsec“ и „mpg“. Обаче е показана още една функция, т.е. Тълкуването става далеч по-лесно с функцията cor.test.
Подобно може да се направи и с другите два метода на корелация:
R код за метода на Pearson:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
R код за метода на Kendall:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
R код за метод на Spearman:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Коефициентът на корелация варира между -1 и 1.
Ако коефициентът на корелация е отрицателен, това означава, когато x се увеличава y намалява.
Ако коефициентът на корелация е нула, това означава, че не съществува връзка между x и y.
Ако коефициентът на корелация е положителен, това означава, когато x се увеличава y също има тенденция да се увеличава.
д) T-тест: T-тестът ще ви каже дали два набора от данни идват от една и съща (ако приемем) нормална дистрибуция или не.
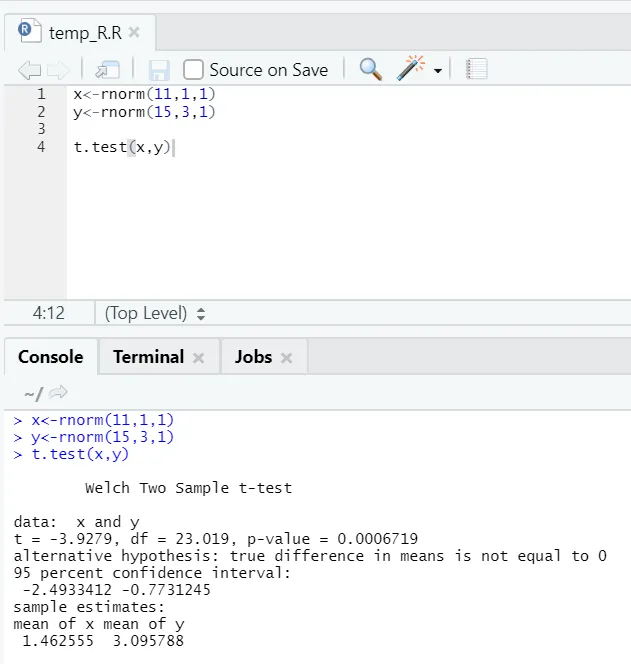
Тук трябва да отхвърлите нулевата хипотеза, че двете средства са равни, тъй като р-стойността е по-малка от 0, 05.
Този показан екземпляр е от тип: несдвоени набори от данни с неравномерни отклонения. По същия начин може да се опита с сдвоения набор от данни.
е) Проста линейна регресия: Това показва връзката между прогнозата / независимата и променливата / зависимата променлива.
Един прост практически пример може да бъде прогнозиране на теглото на човек, ако височината е известна.
R синтаксис
lm(formula, data)
Тук формулата изобразява отношението между изход, т.е. y, и входната променлива iex Данните представляват набора от данни, върху който формулата трябва да се приложи.
Нека да видим един практически пример, където площта на пода е променливата на входа, а наемът е променливата на изхода.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
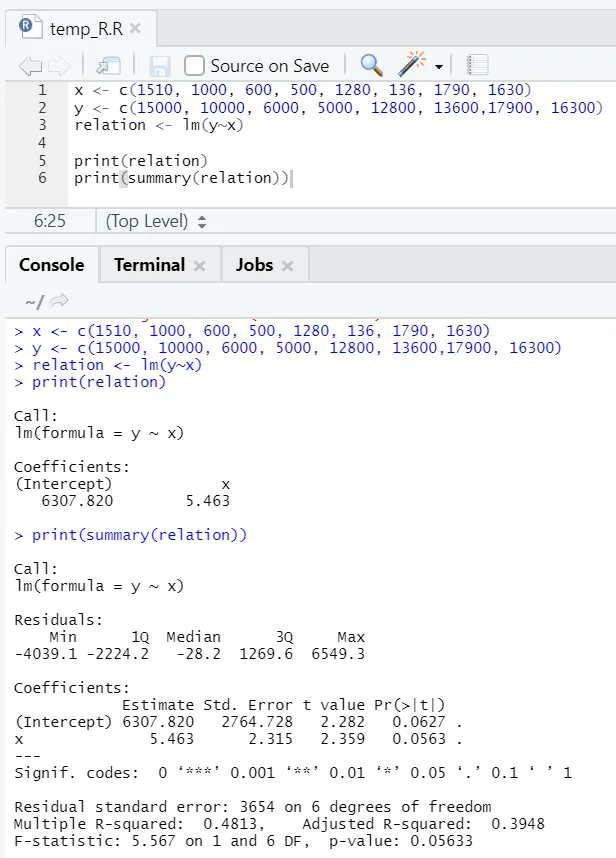
Тук P-стойността е не по-малка от 5%. Следователно нулевата хипотеза не може да бъде отхвърлена. Няма голямо значение за доказване на връзката между етажната площ и наема.
Тук R-квадратната стойност е 0, 4813. Това означава, че само 48% от дисперсията в изходната променлива може да се обясни с входната променлива.
Да кажем, че сега трябва да прогнозираме стойността на етажната площ, въз основа на горепосочения модел.
R код
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
R изход:
След изпълнението на горния R код, изходът ще изглежда както следва:
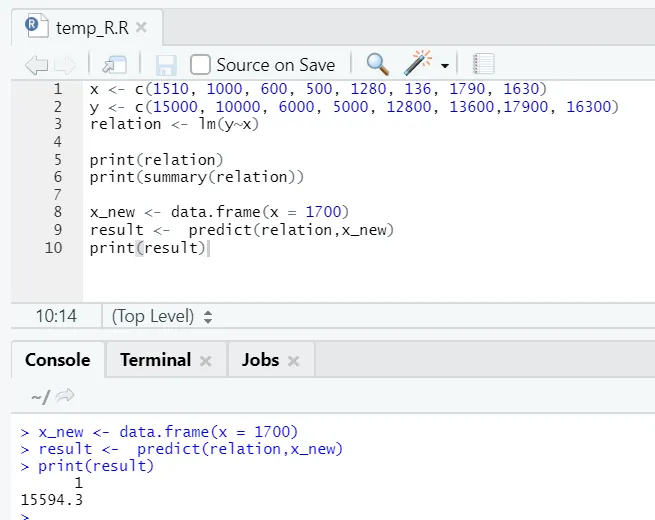
Човек може да пасне и да визуализира регресията. Ето R код за това:
# Дайте име на файла с png диаграма.
png(file = "LinearRegressionSample.png.webp")
# Начертайте диаграмата.
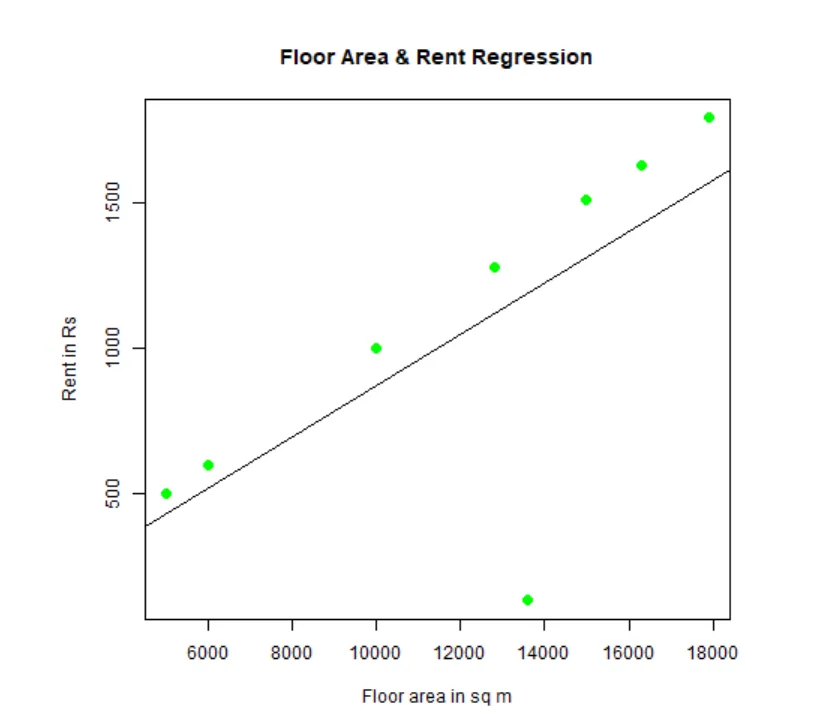
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Запазване на файла.
dev.off()
Тази графика „LinearRegressionSample.png.webp“ ще бъде генерирана в текущата ви работна директория.
ж) Chi-Square тест
Това е статистическа функция в R. Този тест има своето значение, за да се докаже дали съществува корелация между две категорични променливи.
Този тест също работи като всеки друг статистически тест, базиран на p-стойност, човек може да приеме или отхвърли нулевата хипотеза.
R синтаксис
chisq.test(data), /code>
Нека видим един практически пример за това.
R код
# Заредете библиотеката.
library(datasets)
data(iris)
# Създайте рамка от данни от основния набор данни.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Създайте таблица с необходимите променливи.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Извършете тест Chi-Square.
print(chisq.test(iris.data))
R изход:
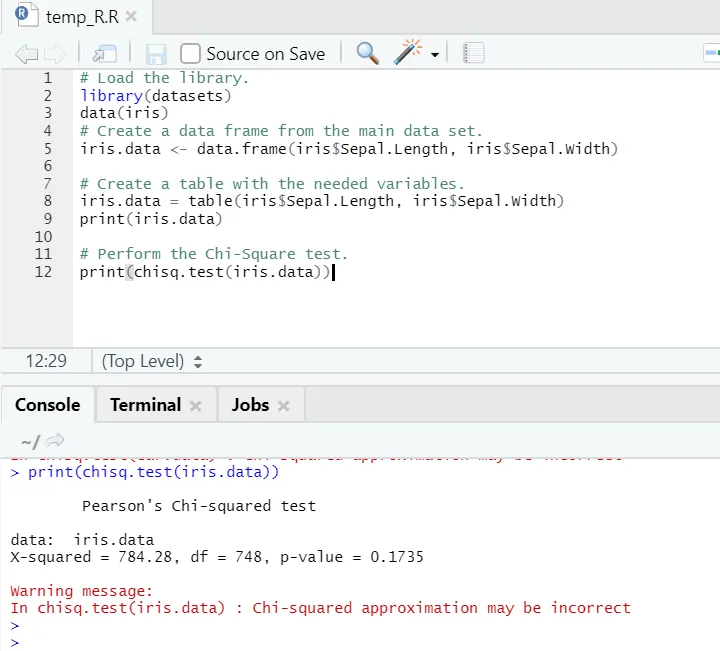
Както се вижда, тестът на квадратен чи е извършен върху набор от данни на ириса, като се имат предвид двете му променливи „Sepal. Дължина “и„ Sepal.Width “.
P-стойността е не по-ниска от 0, 05, следователно корелация не съществува между тези две променливи. Или можем да кажем, че тези две променливи не зависят една от друга.
заключение
Функциите в R са прости, лесни за поставяне, лесни за хващане и същевременно много мощни. Видяхме в Р. различни функции, които се използват като част от основите. След като се почувствате удобно с тези функции, разгледани по-горе, можете да изследвате други разновидности на функциите. Функциите ви помагат, карайте кода да се изпълнява просто и сбито. Функциите могат да бъдат вградени или дефинирани от потребителя, всичко зависи от нуждата, докато адресирате проблем. Функциите придават добра форма на програма.
Препоръчителни статии
Това е ръководство за Функции в R. Тук обсъждаме как да пишем Функции в R и различни видове функции в R със синтаксис и примери. Можете също да разгледате следната статия, за да научите повече -
- R Струнни функции
- SQL стринг функции
- T-SQL стринг функции
- PostgreSQL стринг функции