Excel NORMSINV (Съдържание)
- Въведение в Excel NORMSINV
- Как да използвам NORMSINV формула в Excel?
Въведение в Excel NORMSINV
Функцията на обратното нормално кумулативно разпределение в excel е важен инструмент, който връща обратното нормално кумулативно разпределение за дадена стойност на вероятността, т.е. обикновено връща обратната част на стандартното нормално кумулативно разпределение (което има средно нула и стандартно отклонение от едно) Функцията NORM.S.INV за първи път е въведена във версия на Microsoft excel 2010, която е актуализирана версия на функцията NORMSINV през excel 2013 и най-новата версия. Функцията NORMSINV се използва най-вече за анализ на задълженията и финансов анализ.
Синтаксис на Excel NORMSINV

Аргумент:
Вероятност - Което не е нищо друго, освен вероятността съответства на нормалното разпределение.
Как да използвам NORMSINV формула в Excel?
В Microsoft excel вградената функция NORMSINV е категоризирана по статистическа функция, която е показана на екрана по-долу (където ще изчисли обратната част на нормалното кумулативно разпределение за дадена вероятност).
- Отидете в меню с формули.
- Щракнете върху Още функция, както е показано на снимката по-долу.

- Изберете категория на статистиката под която ще намерим функцията NORM.DIST, както е показано по-долу.
Пример №1 - Използване на NORM.DIST и NORMSINV
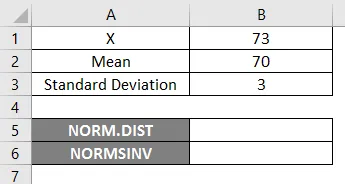
За да използваме функцията NORM.DIST, нека започнем с лесен пример, в който трябва да открием студентските оценки, да предположим, че имаме класния изпит със средна оценка 70, т.е. mu = 70, а стандартното отклонение за класа е 3 точки, т.е. сигма = 3 тук трябва да разберем каква е вероятността учениците да са получили оценките 73 или по-малко, т.е. P (X <= 73). Така че нека да видим как да разберем вероятността с помощта на функцията NORM.DIST.
- X = 3
- Средно = 70
- Стандартно отклонение = 3
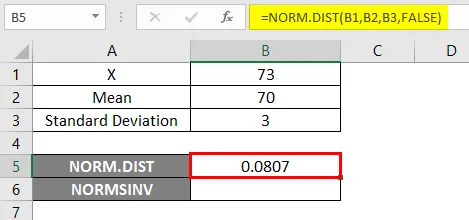
- Приложете функцията NORM.DIST, както е посочено по-долу.
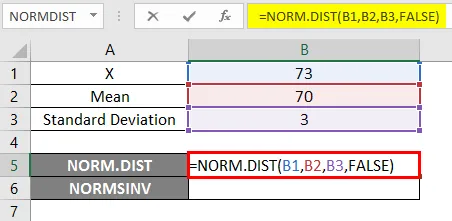
- Ако приложим горната функция NORM.DIST, ще получим вероятността 0, 0807.
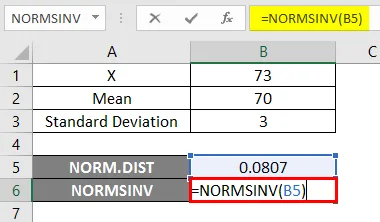
- Сега приложете функцията NORMSINV, за да разберете обратното на нормалното кумулативно разпределение, както е показано по-долу.
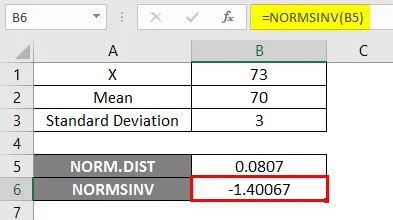
Резултат -
В резултата по-долу можем да видим, че получихме отрицателни стойности -1.40067 за дадената вероятност, т.е. обратно на нормалното кумулативно разпределение.
Пример №2 - Средно и точно стандартно отклонение
Нека видим още един пример с данни на базата на кривата, за да можем да се запознаем със средното и точното стандартно отклонение.
- Средно = 7
- Стандартно отклонение = 1.3
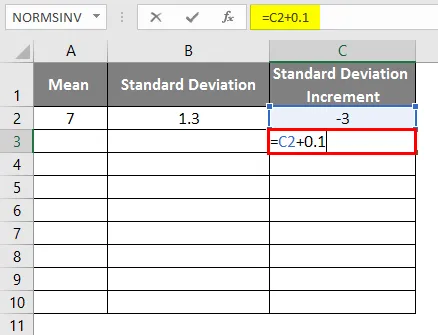
- Стандартно увеличение на отклонението като -3

- За да получим кривата на звънеца, трябва да добавим 0, 1 към увеличение на стандартното отклонение, където данните са както е показано по-долу.
- След прилагане на формулата резултатът е както е показано по-долу.
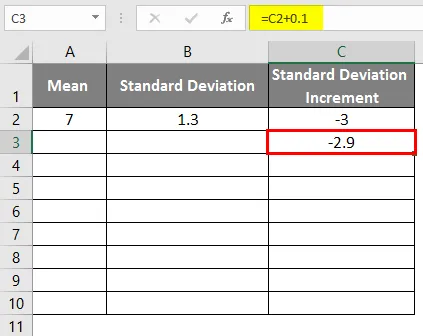
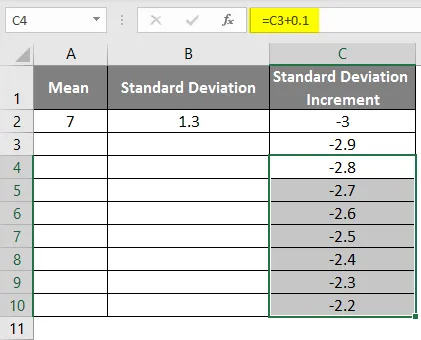
- Плъзнете стойностите, за да получите повече стойности, докато получим положителните стойности, така че да получим лява крива.
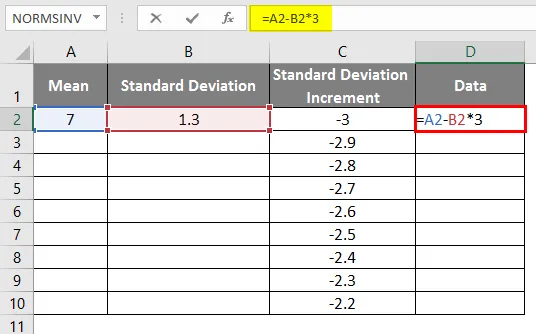
- За да получим правилната крива трябва да приложим формулата като = средно-стандартно отклонение * 3, така че да получим точните криви.
- След използване на формулата резултатът е показан по-долу.
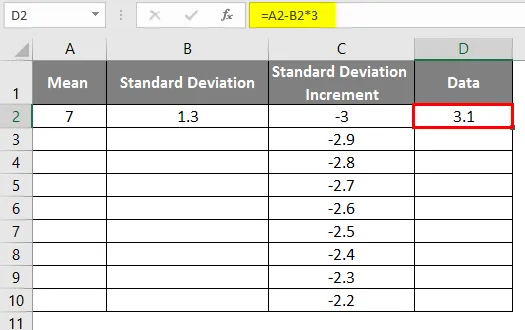
- Както в горните данни за нарастване на стандартното отклонение за получаване на лявата крива, ние увеличихме стойностите с 0, 1
- Същият сценарий се използва, като се прилага формулата като = 3.1 + СТАНДАРТНО УСТРОЙСТВО / 10, за да се получи нарастване на кривата 0, 1
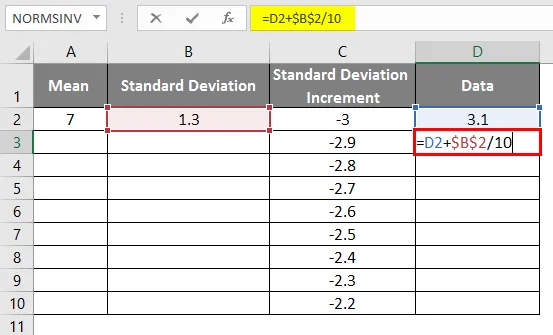
- След използване на формулата резултатът е показан по-долу.

- Плъзнете стойностите, за да получите точния резултат, който е показан на екрана по-долу.
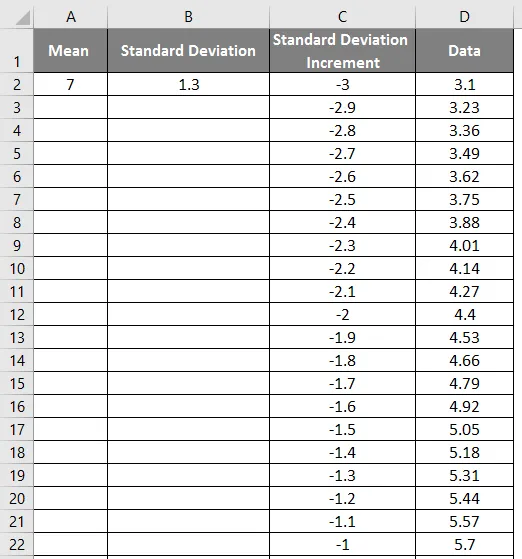
- Сега приложете нормалната функция на разпределение с формулата = NORM.DIST (DATA стойност, средно, стандартно отклонение, невярно).
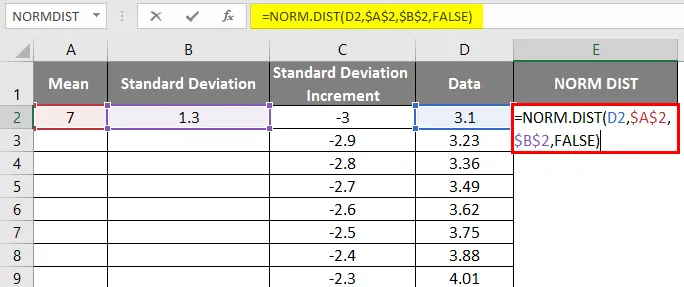
- Ще получим следния резултат, както следва.
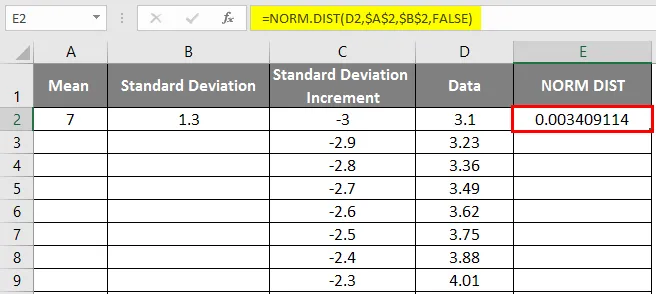
- Плъзнете стойностите, за да получите точния резултат, който е показан по-долу.
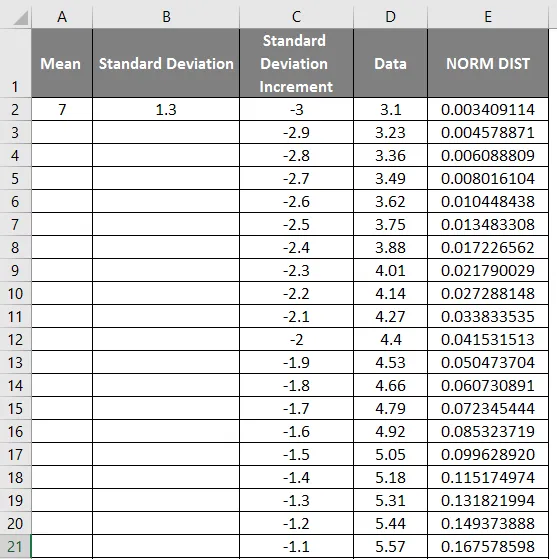
- Както можем да видим на горния екран сме изчислили NORMAL разпределение от средното и стандартното отклонение. Сега нека да видим каква ще бъде обратната на NORMAL разпределение чрез прилагане на NORMSINV, което е показано по-долу.
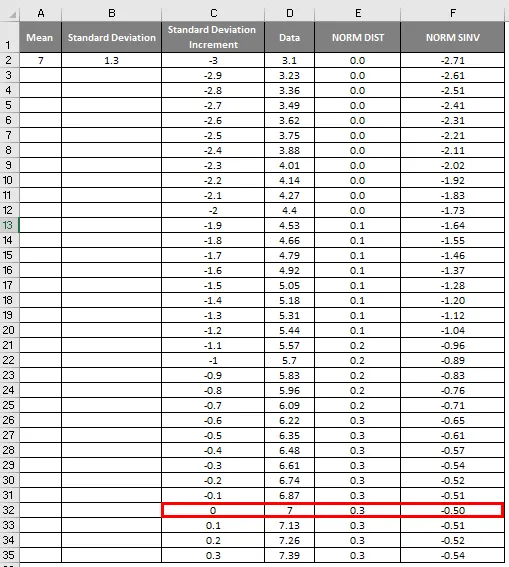
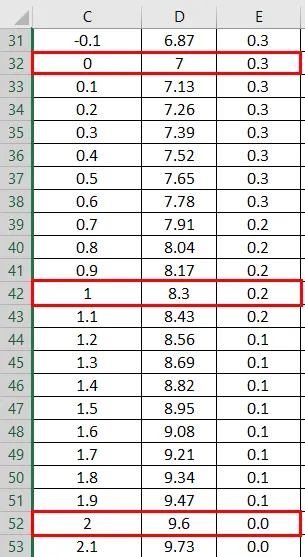
- Тук можем да видим, че Value Zero (0) има стандартно отклонение като 7.

Прилагане на разпръсната графика, за да разгледате как изглежда лявата и дясната крива.
- Първо изберете данните и колоната Normal.
- Отидете на раздела Вмъкване и изберете разпръснатата графика, както следва.
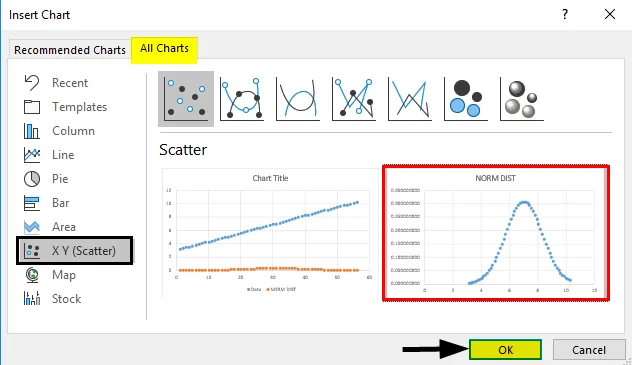
- Ще получим долната графика на кривата, както е показано по-долу.
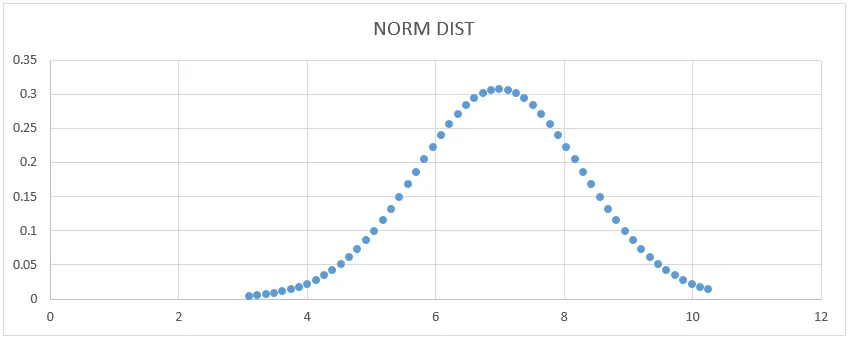
Тук можем да видим, че Средна стойност 7 има стандартна форма на отклонение, където можем да покажем това, като нарисуваме права линия, за да я представим.
- Средно = 7
- 1 –Стандартно отклонение показва 68% от Данните.
- 2 –Стандартното отклонение показва 95% от данните.
- 3 –Стандартното отклонение показва 99, 7% от данните.
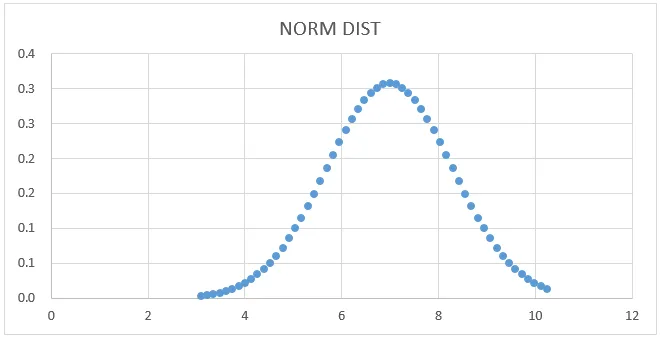
Графика за нормално разпределение:
NORMSINV Графика:
Сега от горната фигура изберете колоната с данни и NORM SINV, за да получите графиката по-долу, както следва.
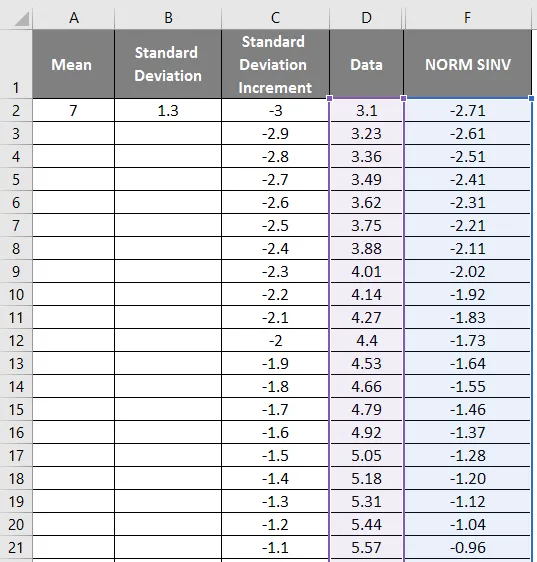
- Първо изберете данните и колоната Normal.
- Отидете на раздела Вмъкване и изберете разпръснатата графика.
- Ще получим графиката по-долу, която е показана на снимката по-долу.
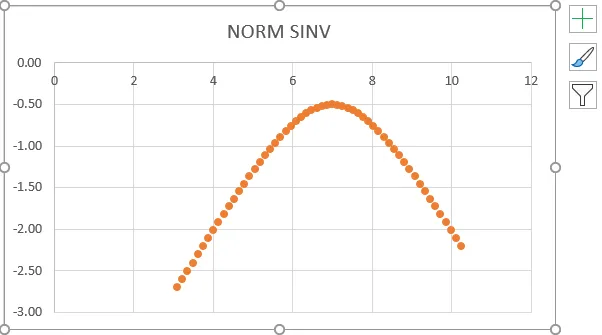
- От горната снимка на екрана можем да видим, че получихме точно обратното на нормалното разпределение, което показва същата цифра на стойността, показана по-долу.

Пример №3 - Конфигуриране на лявата и дясната крива
В този пример ще конфигурираме лявата и дясната крива, използвайки нормалната функция на разпределение. Помислете по-долу данните, както са показани по-долу, където x има отрицателни стойности и се увеличава до положителни стойности.
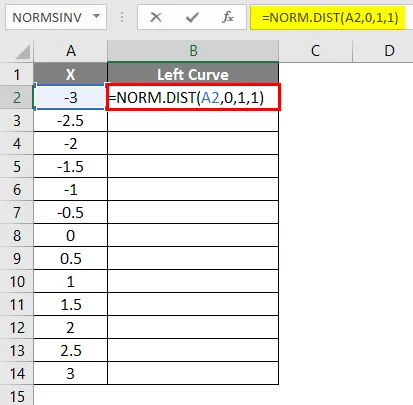
- Прилагайте формулата = NORM.DIST (A2, 0, 1, 1).
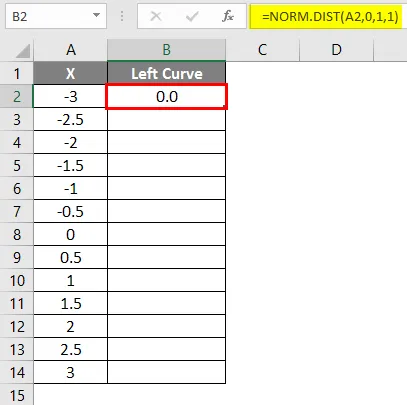
- След прилагане на формулата резултатът е показан по-долу.
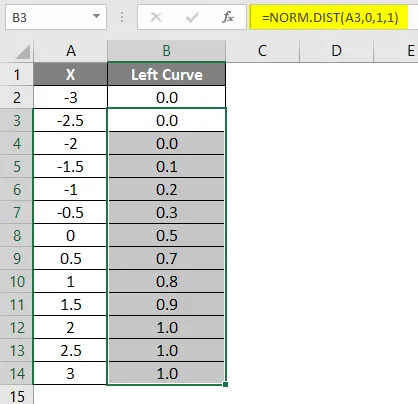
- Плъзнете формулата в други клетки.
- Прилагайте формула = 1-B2 .
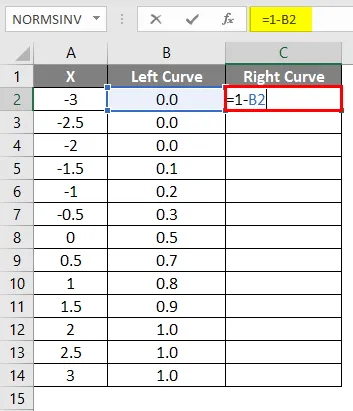
- След прилагане на формула резултатът е показан по-долу.
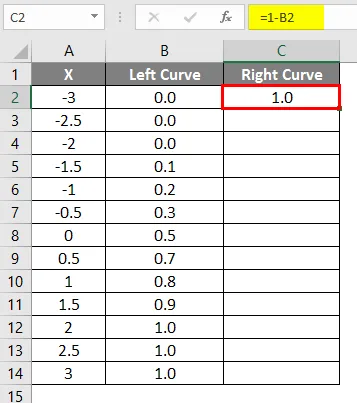
- Плъзнете същата формула в други клетки.
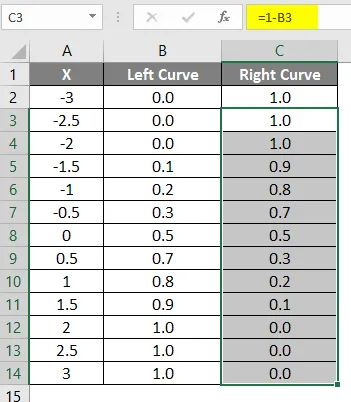
Резултатът от приложената по-горе формула е показан по-долу.
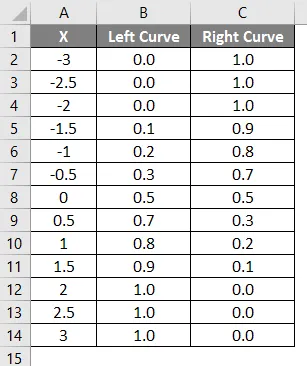
- Стойностите на лявата крива се изчисляват чрез прилагане на формулата NORMAL DISTRIBUTION чрез задаване на кумулативната стойност като True и NORMSINV се изчислява с помощта на лявата крива.
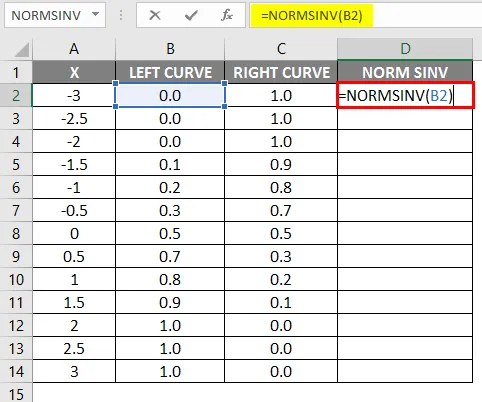
- След прилагане на формулата резултатът е показан по-долу.
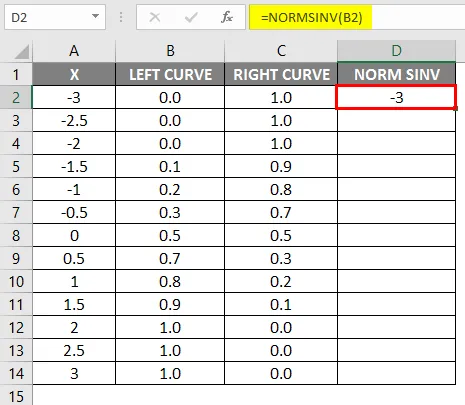
- Плъзнете същата формула в други клетки.
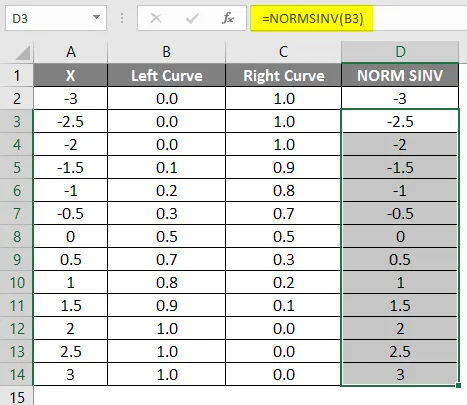
Както виждаме, че получихме същата стойност за NORMSINV, която не е нищо друго, освен обратната на нормалното разпределение. По същия начин ще получим правилната стойност на кривата, като изчислим 1-лявата крива стойност. В следващата стъпка ще проверим как ще получим височината на x, използвайки разпръснатата графика.
- Изберете левия лек и дясната колона на кривата.
- Отидете да вмъкнете меню.
- Изберете разпръснатата графика, както следва.
Ще получим резултата от графиката по-долу, както е показано по-долу.
NORM SINV Графика:
На графиката по-долу можем да видим, че лявата крива на НОРМ РАЗПРЕДЕЛЕНИЕ има точно съвпадение за (0, 0, 5), което лежи в центъра на линията, където ще получим същата графика, ако кандидатстваме за NORMDIST.
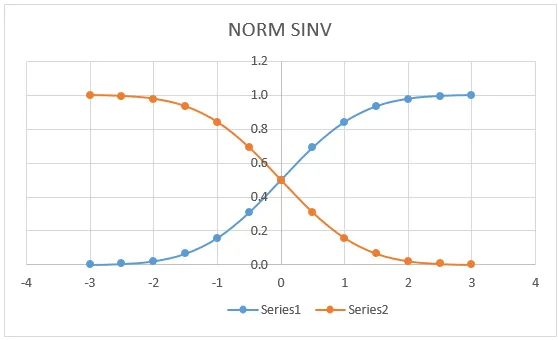
Тук в горната графика много ясно се вижда, че получихме точната средна стойност в централна точка, която обозначава:
- X = 0
- Лява крива = 0, 5
- Дясна крива = 0, 5
Показахме го, за да прегледаме стойностите на NORMSINV в графичен формат, както е показано по-долу.
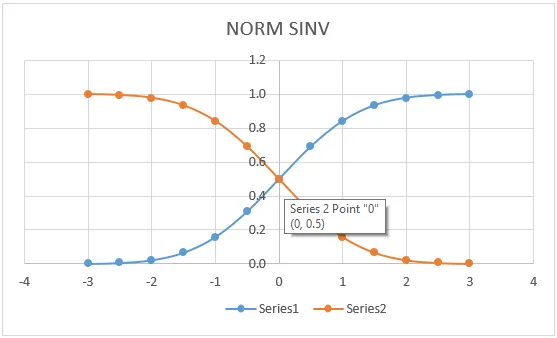
Неща, които трябва да запомните за Excel NORMSINV
- #VALUE! Грешка възниква, когато даденият аргумент е ненумерова или логическа стойност.
- В функцията за нормално разпределение обикновено получаваме #NUM! грешка поради аргумента на стандартното отклонение е по-малка или равна на нула.
Препоръчителни статии
Това е ръководство за Excel NORMSINV. Тук обсъждаме как да използваме NORMSINV в Excel, заедно с практически примери и шаблон за excel за сваляне. Можете да разгледате и другите ни предложени статии -
- Как да използвате полето за име в Excel?
- Работа с Matrix в Excel
- Какво става, ако анализ в Excel
- NPV формула в Excel