Формула за вариация на населението (Съдържание)
- Формула за вариация на населението
- Примери за формула на вариация на населението (с шаблон на Excel)
Формула за вариация на населението
В статистиката отклонение по същество е мярка за намиране на дисперсията на стойностите на набора от данни от средната стойност на набора от данни. Той измерва разстоянието на тази точка от данни и средната стойност. Така че колкото по-голяма е дисперсията, толкова по-голяма ще бъде дисперсията и точките от данни ще имат тенденция далеч от средната стойност. По същия начин, по-ниската дисперсия показва, че точките от данни ще бъдат по-близо до средната. Много е полезно при сравняване на набори от данни, които могат да имат еднаква средна стойност, но различен диапазон. Разминаването на населението в същия смисъл показва как са разпределени точките от данни за населението. Това е средната стойност на разстоянията от всяка точка от данни в популацията до средната стойност в квадрат. Обикновено се изчислява дисперсията на данните за населението, но понякога данните за населението са толкова огромни, че няма смисъл от икономически смисъл да се намери вариацията за това. В този случай се изчислява пробата на извадката и това ще стане представител на дисперсията на популацията.
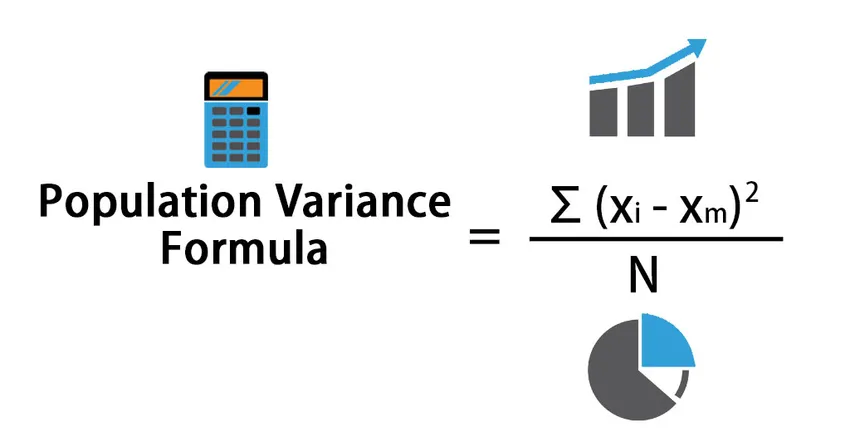
Да предположим, че имате набор от данни за популация X с точки от данни (X1, X2 …… ..Xn). Формулата за вариация на населението се дава от:
Population Variance = Σ (X i – X m ) 2 / N
Където:
- X i - i th стойност на набора от данни
- X m - Средна стойност на набора от данни
- N - Общ брой точки от данни
Формулата може да изглежда объркваща в началото, но наистина трябва да се работи. Следват стъпките, които могат да се следват за изчисляване на вариацията на населението:
- Намерете дали наборът от данни, който работите, е изваден или съвкупност.
- Намерете броя точки в набора от данни, т.е. n за населението.
- Следващата стъпка е да намерите средната стойност. Това е основно средната стойност на всички стойности.
- След това, за всяка точка от данни, намерете разликата на тази от средната стойност и след това я квадрат.
- Вземете сумата на всички стойности в горната стъпка и я разделете на брой точки, изчислени в точка 2.
Има друг начин за изчисляване на дисперсията, като се използва VAR.P () функция за дисперсия на популацията и VAR.S () функция за отклонение на извадката в excel.
Примери за формула на вариация на населението (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на формулата за вариация на населението.
Можете да изтеглите този шаблон за формула на вариантите за вариантите на населението тук - шаблон на вариацията на населението формула ExcelФормула за вариация на населението - Пример №1
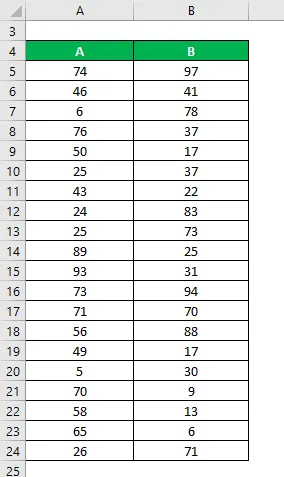
Да речем, че имаме два примерни набора от данни A&B и всеки съдържа 20 произволни точки от данни. Изчислете отклонението на популацията и за двата набора от данни.
Набор данни:
Средната стойност се изчислява като:
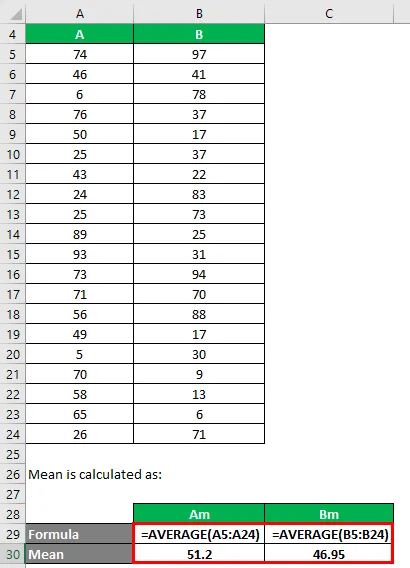
- Средно на набор от данни A = 51.2
- Средно на набор от данни B = 46.95
Сега трябва да изчислим разликата между точките от данни и средната стойност.
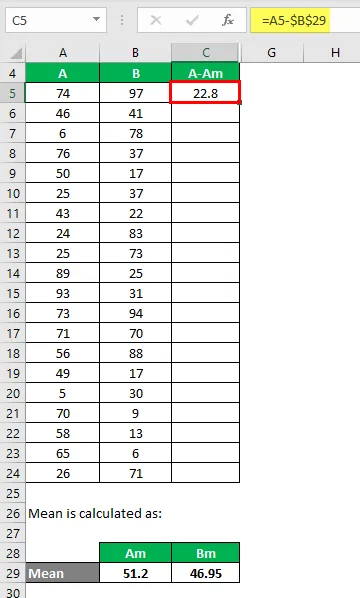
По същия начин, изчислете за всички набори от данни на A.
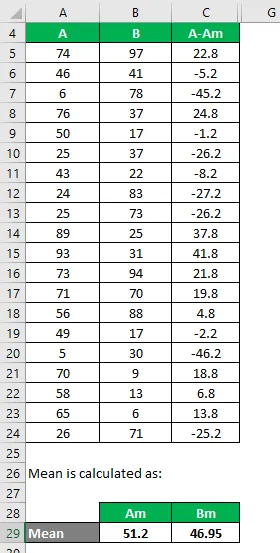
По същия начин, изчислете го и за набор от данни Б.
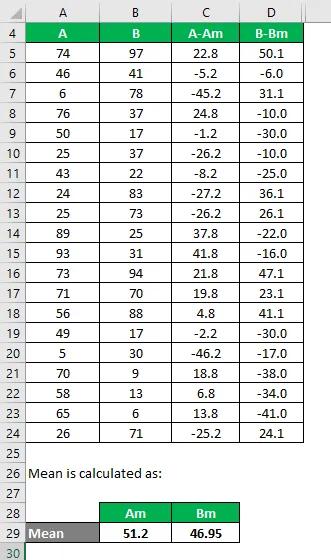
Изчислете квадрата на разликата за двата набора от данни A и B.
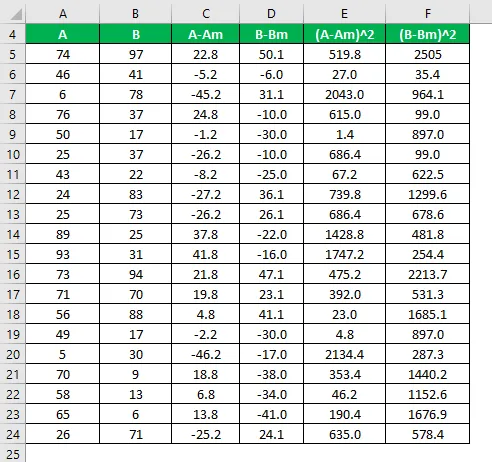
Вариантът на популацията се изчислява по формулата, дадена по-долу
Вариант на популацията = Σ (X i - X m ) 2 / N
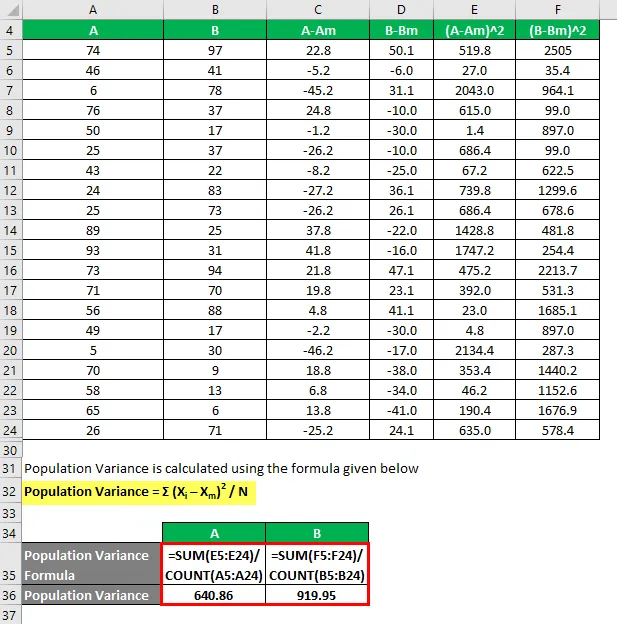
Така че, ако видите тук, B има по-голяма дисперсия от A, което означава, че точките от данни на B са по-разпръснати от A.
Формула за вариация на населението - пример №2
Нека да кажем, че сте много рискован инвеститор и искате да инвестирате пари на фондовия пазар. Тъй като вашият апетит към риск е нисък, искате да инвестирате в безопасни акции, които имат по-малка разлика.
Искате да анализирате запасите въз основа на техните минали резултати, затова решихме да вземем извадка от 15 години и да работим върху тези данни. Вашият финансов съветник ви предложи 4 акции, от които можете да избирате. Искате да изберете 2 акции сред тези 4 и ще решите това на базата на по-ниска дисперсия.
Имате информация за историческите им данни за последните 15 години.
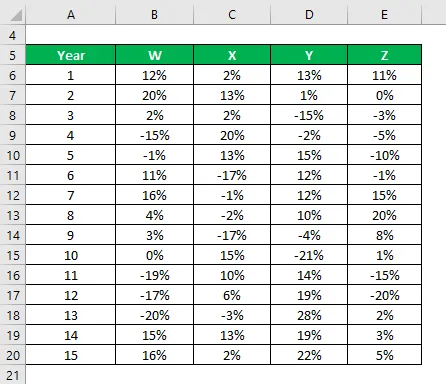
Вариантът на популацията се изчислява с помощта на Excel Formula
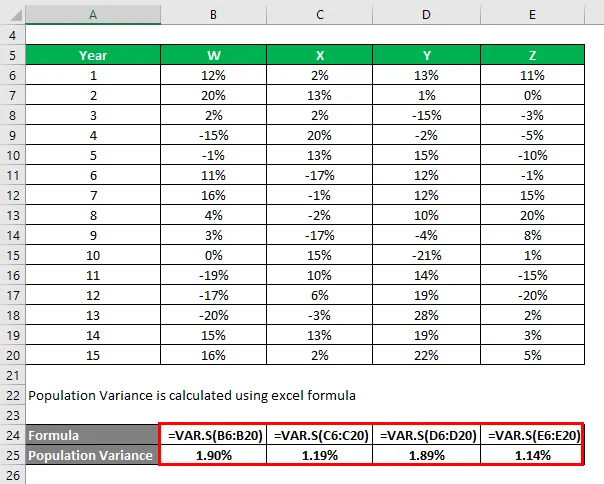
Въз основа на информацията ще изберете акции X и Z, които да инвестирате, тъй като те имат най-ниската дисперсия.
обяснение
Ние обсъждаме значението на отклонението от статистическа гледна точка, но това също ни помага да разберем различни финансови съотношения. Вариантът е основен камък за стандартно отклонение, което се изчислява, като се вземе квадратният корен на дисперсия. Стандартното отклонение е мярка за риска, който инвестицията носи и колко рискова е тази инвестиция. Въз основа на риска, който инвестицията има, инвеститорите след това могат да изчислят минималната възвръщаемост, необходима за компенсиране на този риск. Стойността на вариацията, тъй като е квадрат на число, винаги ще бъде положителна. Това може да бъде нула за набор от данни, който има всички идентични елементи.
Съответствие и използване на формулата за вариация на населението
Вариантът помага на инвеститорите и анализатора да определят стандартното отклонение, което допълнително помага да се намери съотношението на риска и възнаграждението или коефициента на Шарп за инвестиция. По принцип всеки може да спечели безрискова норма на възвръщаемост, като инвестира в хазна и безрискови ценни книжа. Но връщането отгоре и над това е излишната възвръщаемост и да се постигне това.
За да се увеличи коефициентът на Шарп, по-добра е инвестицията.
Както казахме, че дисперсията помага да се намери стандартно отклонение, което измерва риска, но по-ниската стойност на стандартното отклонение не винаги е предпочитана. Ако инвеститор има по-висок риск апетит и иска да инвестира по-агресивно, той ще бъде готов да поеме повече риск и ще предпочете относително по-високо стандартно отклонение от инвеститора, който не изпитва риск. Така че всичко зависи от това какво ниво на риск е готов да поеме инвеститорът.
Препоръчителни статии
Това е ръководство за формулата за вариация на населението. Тук обсъждаме как да изчислим вариацията на популацията заедно с практически примери и изтеглящ се шаблон на excel. Можете също да разгледате следните статии, за да научите повече -
- Ръководство за формула за разпределение на Т
- Примери за относителна стандартна формула за отклонение
- Как да изчислим паритета на покупателната способност?
- Формула за вариация на портфейл