Сложни числа в MATLAB - Как да генерираме сложен номер?

Въведение в сложните числа в MATLAB

Сложните числа са комбинацията от реални числа и въображаеми числа под формата на p + qi, където p и q са реалните числа и i е въображаемото число. Определено е въображаемо число, където i е резултат от уравнение a 2 = -1. Можем да използваме i или j, за да обозначим въображаемите единици. Като сложни числа се използват при всякакви математически изчисления и Matlab се използва главно за извършване на математически изчисления. И така, сложните числа представляват важна част от обучението на Matlab.

Генериране на сложни числа в MATLAB

Сложните числа могат да бъдат създадени или декларирани в Matlab с помощта на 'сложна' функция. Можем също да създадем сложни числа, като намерим квадратния корен на всяко отрицателно число. В Matlab можем да използваме i или j, за да обозначим въображаемата част на комплексното число.

Примери

X = 4 + 5i

Тук X е сложно число, което съдържа 2 части, т.е. реална и въображаема част. 4 е истинската част и 5 е въображаемата част. Можем да намерим истинските и въображаемите части, използвайки функции в Matlab.

a = real (X) = 4 (Това дава реалната част от комплексното число)
b = imag (X) = 5 (Това дава въображаемата част на комплексното число)
комплекс (6, 7) = 6 + 7i (Тази функция се използва за създаване на сложно число)

Също така можем да създадем сложни масиви в Matlab, които също могат да бъдат декларирани с помощта на сложните функции.

a = комплекс (x, y)

Има определени условия за x и y, които трябва да следваме като x и y не трябва да бъдат единични или двойни. Сложен скалар може да се създаде, ако два входа са скаларни по природа като,

X = комплекс (5, 3)
X = 5.0000 + 3.0000i

По същия начин може да се създаде сложен вектор, ако имаме два входа като вектори.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3 5 1; 2));
a = комплекс (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Можем да създадем сложно число със само един скалар,

X = комплекс (10)
X = 10, 0000 + 0, 0000i

Има определени условия, които трябва да следват входните и изходните аргументи,

Входните аргументи съдържат реални и въображаеми части като x всяко y. x и y трябва да бъдат скаларни, векторни, многоизмерни масиви или матрици в MATLAB. размер x и y трябва да са еднакви. Те трябва да са от един и същи тип данни, но има няколко изключения, като двойно може да се използва с единично и цяло число може да се комбинира с двойно, което е скаларно.

Изходът на масива може да бъде векторен, скаларен, матричен или многоизмерен масив в зависимост от входните аргументи. Размерът на изхода трябва да бъде същият като на входа. Ако входните аргументи са с различни типове данни, изходът се определя от,

Ако някой от входните аргументи е единичен по характер, изходът също трябва да бъде единичен.
Ако един от входните аргументи е цяло число по характер, изходът трябва да е от цяло число.

Можем да проверим дали матрицата е истинска или въображаема, като използваме isreal функция.

Код:

X = (2+i, 1); Isreal(X)

изход:

Код:

Isreal (X (2))

изход:

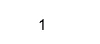
За да извлечем истинските и въображаемите части, можем да използваме реални и имаг функции в Matlab като,

Код:

real(X)

изход:

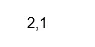
Код:

imag(X)

изход:

Операции и функции на сложни числа в MATLAB

Има няколко операции и функции, които могат да се изпълняват с помощта на сложни числа в Matlab като

abs: Тази функция се използва за намиране на модула на всяко сложно число под формата на p + qi. abs (2 + 3i) = квадратен корен на (2 2 + 3 2) = (13) 0.5
ъгъл: За да намерите фазовия ъгъл на комплексното число.

Има определени съвети, които трябва да се следват за правилното функциониране на сложни числа в Matlab като,

Трябва да избягваме да използваме i и j като част от имена на променливи, тъй като те се използват при обозначаване на въображаемите части от комплексното число.
Трябва да избягваме използването на j или i, ако въображаемата част е 1. Вместо това можем да използваме 1j или 1i.
Можем да създадем сложна функция в Matlab, когато i и j се използват като имена на променливи в някаква част, входните аргументи не са от единичен или двоен тип и въображаемата част е нула.

заключение

Сложните числа се използват в математическата или инженерната област. Много реални или практически приложения могат да бъдат описани с помощта на въображаемата част от сложни числа. Така че разбирането на използването и приложението на сложни числа в различни платформи е важно, особено ако се занимавате с някаква физическа или математическа област.

Препоръчителни статии

Това е ръководство за сложни числа в MATLAB. Тук обсъждаме въвеждането и генерирането на сложни числа в matlab, включително неговите примери с работа и функция. Можете също да разгледате следните статии, за да научите повече-