
Въведение в математическите функции в С
Тази статия изброява различните математически функции, използвани в езиците за програмиране на С с илюстрация на работен код. Компютрите правят огромни математически изчисления и анализи на огромни числа, за да направим това, използвахме математически функции в C. Преди да започнем с, трябва да знаем C езиците да използват заглавието / библиотеката, наречена Math.h за различни математически функции. Това помага при изчисляването на тригонометрични операции, логаритми, абсолютни стойности, квадратни корени. Така че, нека проучим различните видове функции, използвани в тази библиотека. Всички тези функции приемат двойно като тип данни и връщат едно и също.
Различни математически функции в С
Нека да видим различни функции, дефинирани в math.h и библиотеката на Math е категоризирана в три основни типа: тригонометрични функции, математически функции, функции Log / expo. За да се изпълнят функциите по-долу, е задължително да се включи или в кода.
1. етаж (двоен а)
Тази функция връща най-голямото цяло число, не по-голямо от „a“. Той закръглява стойност и връща двойник в резултат. Той се държи различно за отрицателните числа, тъй като те закръглят към следващото отрицателно число.
Например: етаж (7.2) е 7.0
етаж (-7.2) е -8.0
Пример:
Тази програма илюстрира как да изчислите пода за декларираната стойност и закръгля до следващата стойност 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
изход:

2. таван ()
Синтаксис:
double ceil (double b)
Тази функция връща най-малката цяло число, която е по-голяма или равна на b, и закръгля стойността нагоре. За отрицателна стойност се движи вляво. Пример 3.4 връща -3 има изход.
Пример:
Тази програма обяснява, като приема в аргумента float и връща стойността на тавана.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
изход:

3. Sqrt ()
Тази функция връща квадратния корен на определено число.
Синтаксис:
sqrt( arg)
Пример:
Кодът по-долу обяснява най-известната математическа функция sqrt (), като се вземат стойности 'n' за изчисляване на квадратния корен за различните стойности 'n'.
#include
#include
int main()
(
double n, output;
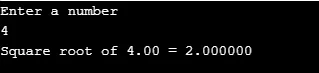
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
изход:
4. кръг ()
Тази функция закръгля най-близката стойност на даден вход. Той изхвърля грешката, ако стойността е твърде голяма. Други функции като lround (), llround () също закръглят най-близкото цяло число.
Синтаксис:
int round(arg)
Пример:
Кодът по-долу е много прост, което се закръгля до най-близката стойност 'r' в цикъла for.
#include
#include
int main ()
(
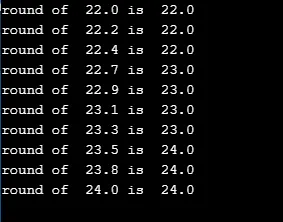
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
изход:
5.pow ()
Тази функция връща захранването за даденото число (a b ). Той връща повдигнато на силата на b, което има два параметъра база и експонент.
Пример:
В изходния код по-долу позволяваме на потребителя да въведе входна стойност, за да изчисли силата на дадените два аргумента.
#include
#include
int main()
(
int r, ba, expr;
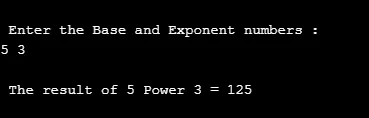
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
изход:
6. trun ()
Тази функция помага при съкращаването на дадената стойност. Тя връща цели числа. За съкращаване на плаващи и двойни стойности се използват truncf (), truncl ().
Синтаксис:
double trunc(a);
Пример:
По-долу изходният код взема две входни стойности a, b, за да отсече двойните стойности.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
изход:

7. fmod ()
Тази функция връща остатъка за дадените две входни стойности, когато m се дели на n.
Синтаксис:
double fmod(double I, double j)
Пример:
В примера по-долу са нужни две стойности от потребителя, за да се изчисли остатъкът с помощта на fmod () функция.
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
изход:

Тригонометрични функции
По-долу са описани различните функции на тригонометричния:
1. грех ()
Тази вградена функция дава задължителна стойност на даденото число, изчислява стойности с плаваща запетая. asin () изчислява дъга, за хиперболични е sinh ().
Синтаксис:
return type sin(y);
y връща стойността в радиани, а типът връщане отнема двойно.
Пример:
В следния изходен код взех две различни входни стойности, за да изчисля грешната стойност и връща двойно.
#include
#include
int main()
(
double a;
double z;
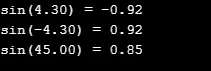
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
изход:
2. sinh ()
Тази математическа функция изчислява тригонометрична допирателна синусова стойност за даденото число.
Синтаксис:
double sinh(x);
пример
В изходния код по-долу синусовият хипербол се изчислява чрез деклариране на входна стойност.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
продукция

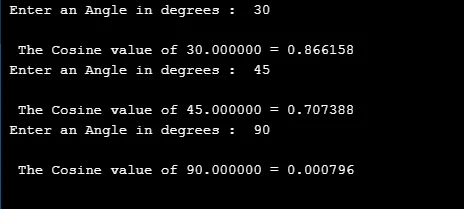
3. cos ()
Тази математическа функция определя тригонометричната косинусна стойност за дадения елемент.
Синтаксис: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
изход:
4. cosh ()
Той връща хиберболичен косинус за дадена стойност.
Синтаксис:
double cosh(y);
пример
Примерът по-долу показва, че са необходими две различни входни стойности за изчисляване на хиперболични.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
продукция

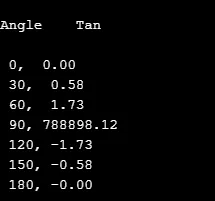
5. тен ()
Тази математическа функция изчислява допирателните стойности на ъгъла за математическия израз и се измерва в радиани.
Тя може да бъде декларирана като
double tan(arguments);
пример
В следния изходен код, тен стойността се изчислява за следните ъгли, които се увеличават с помощта на цикъл.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
изход:
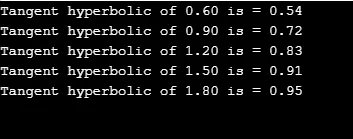
6. tanh ()
tanh () функция връща хиперболична тангента на дадената стойност. Това отнема един параметър. В допълнение за намиране на тангента за дълги двойни и плаващи tanhl () и tanhf () се използват за изчисляване.
Синтаксис:
double tanh( val);
Пример:
Тангентен хиберболичен се изчислява за 'j' стойности, използващи за контури. Нека да видим как работи.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
изход:
Влезте в аритметичните функции
По-долу са описани различните функции на аритметиката на дневника:
1. exp ()
Тази функция извършва изчисляване на експоненциална за дадена стойност (e x ). Има и други подтипове като frexp (), Idexp (), връщащи мантиса и умножени до силата на x.
Синтаксис:
return type exp(value);
Пример:
Програмата взема числова стойност от потребителя, за да изчисли експонента за дадена стойност и връща двойно.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
продукция

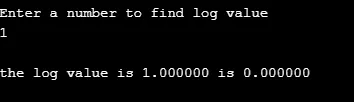
2. log ()
Тази функция връща стойността на логаритъм на дадено число. (към основния e. log e )
Синтаксис:
double log(arg);
Пример:
В следващия пример стойността на лога за даденото число се изчислява с помощта на функция. Дефинираната от потребителя функция lgm () прави изчисления и функция се извиква в основната функция.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
изход:
заключение
В заключение видяхме различни математически функции, използвани в програмирането на С и това са директните библиотечни функции, които трябва да се използват. Програмите на C използват тези функции за различни математически операции. За решаване на някои сложни версии на изчисления тази вградена функция облагодетелства математически ориентиран език за програмиране, за да върне прости стойности.
Препоръчителни статии
Това е ръководство за математическите функции в C. Тук обсъждаме различни математически функции в C с примери. Можете да разгледате и другите ни предложени статии -
- PHP математически функции
- JavaScript математически функции
- Функции за трансфер в Matlab
- Функции на стринг JavaScript
- Въведение в математическите функции в Python
- Преглед на математическите функции в C #
- C Матрично умножение на програмиране
- Квадратни корени в PHP
- Примери за квадратен корен в JavaScript