
Разлика между Z резултат срещу T резултат
Z резултатът е преобразуване на сурови данни в стандартен резултат, когато преобразуването се основава на средната стойност на населението и стандартното отклонение на населението. Когато при нас е наличен пълен набор от данни, можем да изчислим оценката Z. Z резултатът е изваждането на средното население от суровия резултат и след това се разделя резултатът със стандартното отклонение на популацията. T резултатът е преобразуване на сурови данни в стандартния резултат, когато преобразуването се основава на средната проба и стандартното отклонение на извадката. Когато наборът от данни за населението не е налице, трябва да вземем някои примерни данни, за да изчислим средната проба и стандартното отклонение на популацията.
Z резултат
При нормално разпределение, при което са налични пълни данни, това е разстояние от средната стойност. Формулата му е както е дадена по-долу,
Z= (x-μ)/σ
Където,
X = индивидуални необработени данни
μ = Средна популация
σ = Население стандартно отклонение
T резултат
T резултатът е изваждането на индивидуалното стандартно отклонение от индивидуалната средна стойност и след това се разделя резултатът със стандартното отклонение на извадката, цял резултат, умножен по размер на пробата. Формулата му е както е дадена по-долу,
t = ((- μ)/s)*
= примерна средна стойност
μ = Средна популация
s = проба Стандартно отклонение
n = размер на пробата
Нека вземем пример, за да разберем същото по-добре:
В статия има 3 подразделения - I, II и III. Нека броят на студентите, които са отговорили, аз правилно ще бъде 25%, т.е. 75% не са в състояние правилно да отговорят. По същия начин, нека 10% и 20% от броя на хората, които са отговорили правилно на раздели II и III, следователно 90% и 80% са намерили раздел II и III все пак. Предполагаме, че способността, измерена от тези три елемента, е една и съща и тя обикновено се разпределя,
Резултатът за всеки ученик в клас се използва за изчисляване на средната стойност на оценките, която е равна на 50 и стандартно отклонение от 10. Можем да изчислим оценката на Z с резултат 50 като (50-50) / 10 = 0
Можем да тълкуваме, че оценката на ученика е 0 разстояние (в единици от стандартни отклонения) от средната стойност, така че студентът е оценил средно.
Ако резултатът е 60, Z резултатът е (60-50) / 10 = 1
Можем да тълкуваме, че ученикът е отбелязал над средното ниво - разстояние от 1 стандартно отклонение над средното.
Сравнение между главата на резултата Z и T (Инфографика)
По-долу е топ 9 разликата между Z резултат срещу T резултат 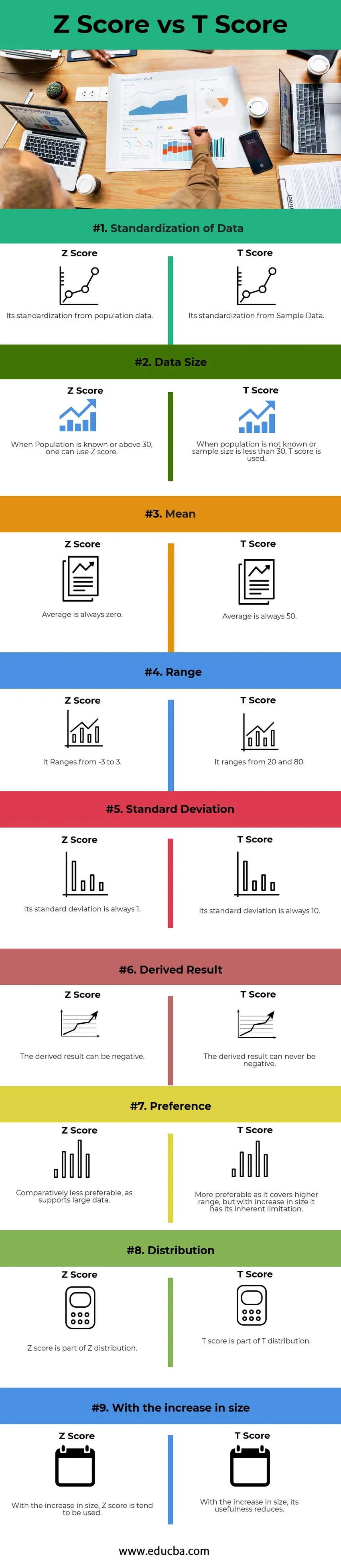
Ключови разлики между Z резултат срещу T резултат
Нека да обсъдим някои от основните разлики между Z резултат срещу T резултат
- Z резултатът е стандартизацията от суровите данни от популацията или повече от 30 извадкови данни към стандартен резултат, докато Т резултатът е стандартизация от извадковите данни на по-малко от 30 данни към стандартен резултат
- Z резултатът варира от -3 до 3, докато резултатът T варира от 20 до 80.
- С увеличаването на размера на данните разпределението има тенденция да бъде Z разпределение. И разпределението на Z оценка срещу T е част от нормалното разпределение, но въз основа на размера, който се различават един от друг
- На практика Z резултатът се използва широко в данните на фондовите борси и за проверка на шансовете на компания да фалира, докато t резултатът се използва широко при проверка на костната минерална плътност и оценката на риска от фрактури
Таблица за сравнение Z резултат срещу T резултат
Нека да разгледаме топ 9 Сравнение между Z резултат и T резултат
| Ср. № | Точки за сравнение | Z резултат | T резултат |
| 1 | Стандартизация на данните | Стандартизирането му от данните за населението | Неговата стандартизация от примерни данни |
| 2 | Размер на данните | Когато населението е известно или над 30, може да се използва Z резултат | Когато популацията не е известна или размерът на извадката е по-малък от 30, се използва оценка Т. |
| 3 | Означава | Средната стойност винаги е нула. | Средно винаги е 50. |
| 4 | диапазон | Той варира от -3 до 3. | Тя варира от 20 и 80. |
| 5 | Стандартно отклонение | Стандартното му отклонение винаги е 1 | Стандартното му отклонение винаги е 10 |
| 6 | Получен резултат | Полученият резултат може да бъде отрицателен | Полученият резултат никога не може да бъде отрицателен |
| 7 | Предпочитание | Сравнително по-малко за предпочитане, тъй като поддържа големи данни | По-предпочитано, тъй като обхваща по-голям обхват, но с увеличаване на размера има присъщото си ограничение |
| 8 | разпределение | Z резултатът е част от Z разпределението | T резултатът е част от разпределението на Т |
| 9 | С увеличаването на размера | С увеличаването на размера Z оценката има тенденция да се използва | С увеличаването на размера полезността му намалява. |
заключение
И двата Z оценка срещу Т резултат са част от тестването на хипотези при нормалното разпределение. Ако имате набор от измервателни оценки за различни мерки, използвайки Z-резултати, можете да кажете как резултатите се поставят в техните разпределения. Тогава можете да ги сравните. Стандартизацията на оценките е широко използвана процедура в областта на изследванията и планирането, тъй като те помагат при сравняване на различни тестови оценки. Стандартизирането на оценките преди комбинирането им помага на изследователя да постигне по-добри и съпоставими резултати.
Препоръчителни статии
Това е ръководство за най-високата разлика между Z резултат срещу T резултат. Тук също обсъждаме ключовите разлики в резултата от Z спрямо T с таблица за инфографики и сравнение. Може да разгледате и следните статии, за да научите повече-
- Финанси срещу икономика - най-добра разлика
- Дефицит срещу дълг - кой е по-добър
- Покупка на активи срещу Покупка на активи
- Паричен пазар срещу капиталов пазар
- Преглед на оценката на Altman Z