
Формула за оценка на Z (Съдържание)
- формула
- Примери
- калкулатор
Какво е формулата на Z Score?
„Z оценка“ е един от най-широко използваните статистически инструменти, който се използва за стандартизиране на резултата, при условие, че средствата от населението са известни и стандартното отклонение. Като такъв, оценката Z е известна и като стандартна оценка. Оценката Z варира в диапазона от -3 пъти стандартното отклонение до +3 пъти повече от стандартното отклонение със средна стойност нула и стандартно отклонение от единица. Формулата за оценка на Z на променлива може да бъде получена чрез изваждане на средната стойност на съвкупността от дадената променлива (която е част от набора от данни или съвкупност) и след това разделянето на резултата чрез стандартното отклонение на съвкупността. Математически той е представен като
Z = (X – μ) / σ
където,
- X = променлива от популацията
- μ = Средна стойност на населението
- σ = Стандартно отклонение на популацията
Примери на формула за оценка на Z (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на оценката Z.
Можете да изтеглите този шаблон за формула за формуляр на Ex Score тук - шаблон за формула за формуляр на Ex ScoreZ формула за оценка - пример №1
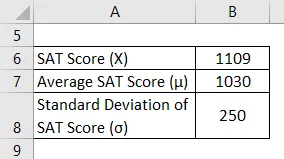
Нека вземем за пример Мани, който наскоро се яви за SAT. Той успя да вкара 1109 в този опит. Въпреки това, според наличната информация, средният резултат за SAT остана около 1030 със стандартно отклонение от 250. Изчислете Z оценката за SAT резултата на Мани и преценете колко добре се справи в сравнение със средните участници в теста.
Решение:
Z Оценката се изчислява по формулата, дадена по-долу
Z = (X - µ) / σ
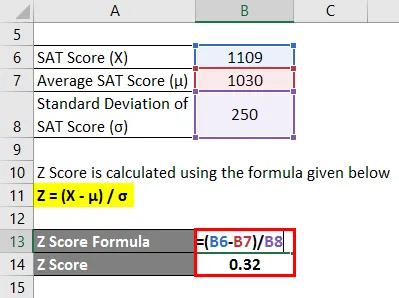
- Z резултат = (1109 - 1030) / 250
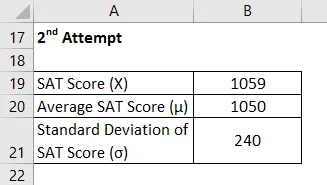
- Z резултат = 0, 32
Следователно SAT резултатът на Мани е с 0, 32 стандартно отклонение по-висок от средния резултат на участниците в тестовете, което показва, че 62, 55% от участниците в тестовете са получили по-малко резултати от Мани.
Z Формула за оценка - пример №2
Нека сега вземем за пример Челси, която два пъти е написала SAT и иска да сравнява представянето си в тях. Тя успя да отбележи 1085 и 1059 при първия си и втория опит съответно. Според наличната информация средният резултат и стандартното отклонение по време на първия опит са съответно 1100 и 230, докато в последния той е съответно 1050 и 240. Моля, помогнете на Челси да реши на кой изпит се представи по-добре.
Решение:
1- ви опит
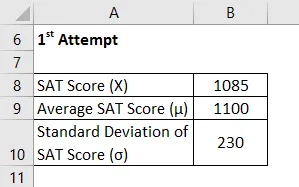
Z Оценката се изчислява по формулата, дадена по-долу
Z = (X - µ) / σ
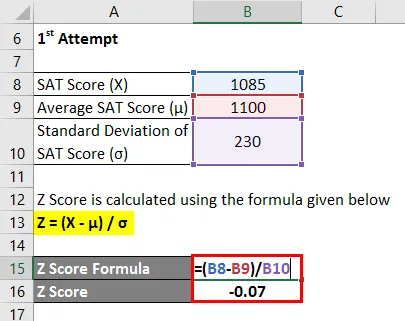
- Z резултат = (1085 - 1100) / 230
- Z резултат = -0.07
Следователно SAT резултатът на Челси в първия опит е 0, 07 стандартно отклонение по-нисък от средния резултат на участниците в теста, което показва, че 47, 40% от участниците в теста са отбелязали по-малко от Челси по време на първия опит.
2- ри опит
Z Оценката се изчислява по формулата, дадена по-долу
Z = (X - µ) / σ
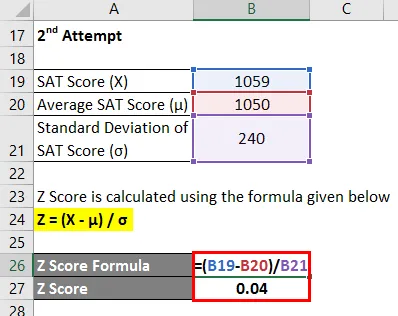
- Z резултат = (1059 - 1050) / 240
- Z резултат = 0, 04
Следователно SAT резултатът на Челси при втория опит е 0, 04 стандартно отклонение по-висок от средния резултат на участниците в тестовете, което показва, че 51.50% от участниците в теста са отбелязали по-малко от Челси по време на втория опит.
Така че от сравнението на оценките на Z става ясно, че Челси се представи по-добре по време на втория си опит.
обяснение
Формулата за оценка на Z може да бъде получена чрез следните стъпки:
Стъпка 1: Първо, изградете популация с голям брой променливи и променливите се означават с X i .
Стъпка 2: След това се изчислява броят на променливите в популацията и се обозначава с N.
Стъпка 3: След това средната стойност на съвкупността се изчислява чрез сумиране на всички променливи, последвани от разделяне на общия брой променливи (стъпка 2) в набора от данни. Средната стойност на популацията се обозначава с μ.
μ = ∑ X i / N
Стъпка 4: След това извадете средната стойност от всяка променлива от набора от данни, за да изчислите тяхното отклонение от средната стойност.
т.е. (X i - μ) е отклонението за i -тата точка от данни.
Стъпка 5: След това изчислете отклоненията в квадрат за променливите, т.е. (X i - μ) 2 .
Стъпка 6: След това добавете всички квадратни отклонения и след това разделете общото на броя на променливите в набора от данни, за да стигнете до дисперсията.
σ 2 = ∑ (X i - μ) 2 / N
Стъпка 7: След това стандартното отклонение на популацията се изчислява чрез изчисляване на квадратния корен на дисперсията, изчислена в горния етап.
σ = √ ∑ (X i - μ) 2 / N
Стъпка 8: Накрая, формулата за оценка на Z се извлича, като се извади средната стойност на съвкупността (стъпка 3) от променливата и след това се раздели резултатът от стандартното отклонение на популацията (стъпка 7), както е показано по-долу.
Z = (X - µ) / σ
Уместност и употреба на формулата за оценка на Z
От гледна точка на статистиката понятието Z оценка е много важно, тъй като е полезно при определяне на вероятността дали дадено събитие ще се случи в рамките на нормално разпределение. Всъщност Z оценката се използва и за сравняване на две сурови резултати от две различни нормални разпределения и това става чрез преобразуване на суровите резултати в Z резултат или стандартизиран резултат. Освен това, положителната Z оценка означава резултат, който е по-висок от средния, докато отрицателният Z резултат означава резултат, по-малък от средния.
Z Калкулатор на формула за оценка
Можете да използвате следния Z Score Formula Calculator
| х | |
| μ | |
| σ | |
| Z | |
| Z = |
|
|
Препоръчителни статии
Това е ръководство за формулата на Z Score. Тук обсъждаме как да изчислим Z резултат заедно с практически примери. Ние също така предлагаме калкулатор Z Score със свалящ се шаблон за excel. Можете също да разгледате следните статии, за да научите повече -
- Примери за формула за размер на пробата
- Как да изчислим средно претегленото?
- Калкулатор за формула на корелация
- Формула за изчисляване на нормалното разпределение
- Примери за Altman Z Score