
Въведение в алгоритма на DFS
DFS е известен като алгоритъм на дълбочината на първо търсене, който осигурява стъпките за преминаване на всеки възел на графика, без да се повтаря никой възел. Този алгоритъм е същият като дълбочината на първото преминаване за дърво, но се различава в поддържането на булева информация, за да провери дали възелът вече е посетен или не. Това е важно за преминаването на графиката, тъй като в графиката има и цикли. В този алгоритъм се поддържа стек за съхраняване на спрените възли по време на преминаване. Наречен е така, защото първо пътуваме до дълбочината на всеки съседен възел и след това продължаваме да обикаляме друг съседен възел.
Обяснете алгоритъма на DFS
Този алгоритъм противоречи на BFS алгоритъма, при който всички съседни възли се посещават, последвани от съседи на съседните възли. Започва изследване на графиката от един възел и изследва нейната дълбочина, преди да се върне назад. В този алгоритъм са разгледани две неща:
- Посещение на върха : Избор на върха или възел на графиката за преминаване.
- Изследване на върха : преминаване през всички възли в съседство с тази върха.
Псевдокод за първо търсене :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Линеен траверс съществува и за DFS, който може да бъде реализиран по 3 начина:
- Предварителна поръчка
- Inorder
- PostOrder
Обратната поръчка е много полезен начин за преминаване и използван при топологично сортиране, както и при различни анализи. Поддържа се и стек за съхранение на възлите, чието проучване все още е в очакване.
Преминаване на графика в DFS
В DFS са следвани стъпките по-долу за преминаване на графиката. Например, дадена графика, нека да започнем от преминаване от 1:
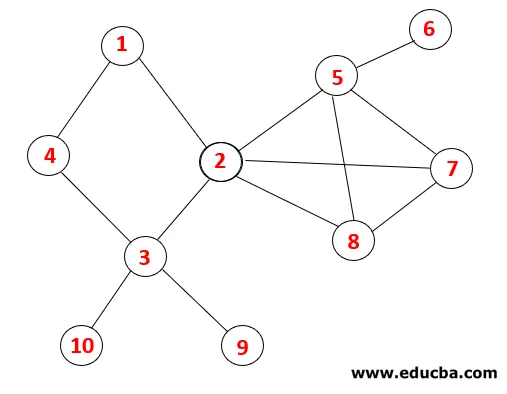
| купчина | Последователност на траверса | Продължително дърво |
| 1 |  |
|
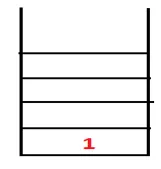 | 1, 4 |  |
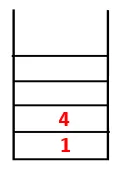 | 1, 4, 3 |  |
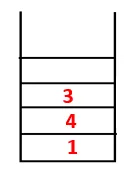 | 1, 4, 3, 10 | 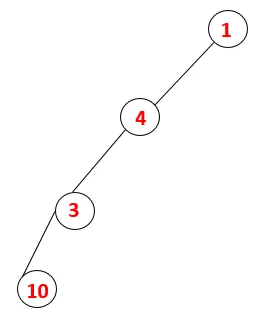 |
 | 1, 4, 3, 10, 9 | 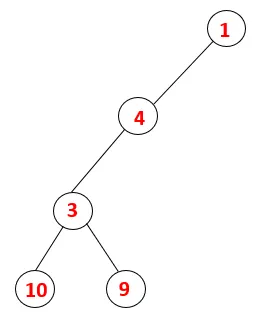 |
 | 1, 4, 3, 10, 9, 2 | 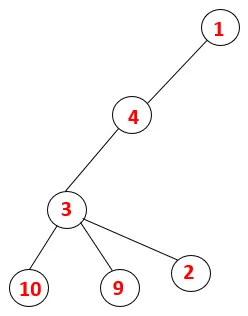 |
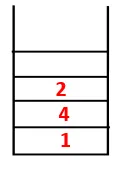 | 1, 4, 3, 10, 9, 2, 8 |  |
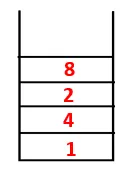 | 1, 4, 3, 10, 9, 2, 8, 7 | 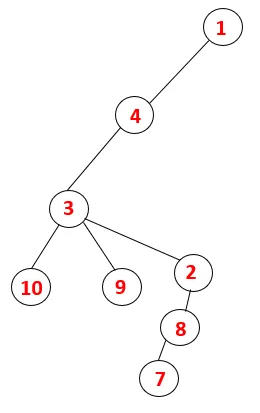 |
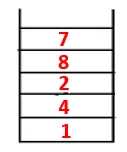 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
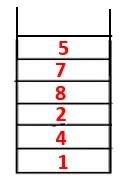 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 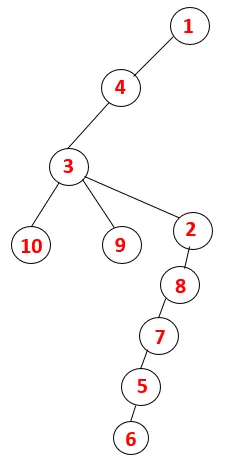 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 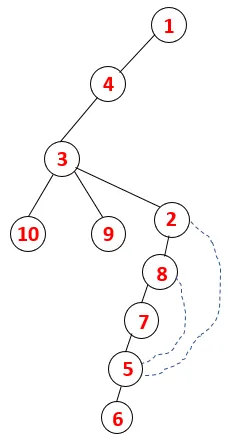 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
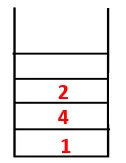 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 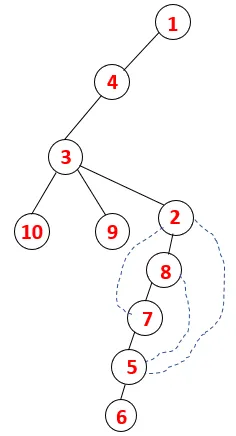 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 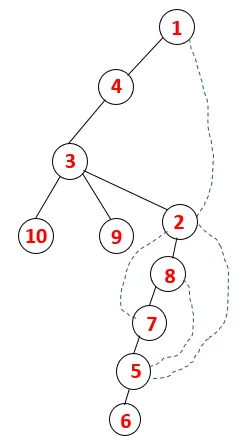 |
Обяснение към алгоритма на DFS
По-долу са стъпките към алгоритъма на DFS с предимства и недостатъци:
Стъпка 1: Възел 1 се посещава и се добавя към последователността, както и към обхващащото дърво.
Стъпка 2: Съседните възли от 1 се изследват, което е 4, като по този начин 1 се изтласква до стека и 4 се изтласква в последователността, както и обхващащото дърво.
Стъпка: Един от съседните възли на 4 се изследва и по този начин 4 се изтласква към стека, а 3 влиза в дървото за последователност и обхващащо.
Стъпка 4: Съседни възли от 3 се изследват, като се натискат върху стека и 10 влиза в последователността. Тъй като няма съседен възел до 10, по този начин 3 се изскача от стека.
Стъпка 5: Друг съседен възел от 3 се изследва и 3 се натиска върху стека и 9 се посещава. Нито един съседен възел от 9 по този начин 3 не е изскочен и последният съседен възел от 3, т.е.
Подобен процес се следва за всички възли, докато стекът не се изпразни, което показва условието за спиране на алгоритъма за преминаване. - -> пунктирани линии в обхващащото дърво се отнасят до задните ръбове, присъстващи в графиката.
По този начин всички възли в графиката се пресичат, без да се повтаря нито един от възлите.
Предимства и недостатъци
- Предимства: Тези изисквания за памет за този алгоритъм са много по-малко. По-малка сложност на пространството и времето от BFS.
- Недостатъци: Решението не е гарантирано Приложения. Топологично сортиране. Намиране на мостове на графика.
Пример за внедряване на DFS алгоритъм
По-долу е примерът за внедряване на алгоритъм DFS:
Код:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
изход:
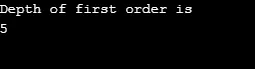
Обяснение към горната програма: Направихме графика с 5 вершини (0, 1, 2, 3, 4) и използвахме посетен масив, за да следим всички посетени върхове. След това за всеки възел, чиито съседни възли съществуват един и същ алгоритъм се повтаря, докато всички възли са посетени. След това алгоритъмът се връща към върха на повикване и го изскача от стека.
заключение
Изискването за памет на тази графика е по-малко в сравнение с BFS, тъй като е необходим само един стек, за да се поддържа. В резултат на това се генерира DFS обхващащо дърво и преминаваща последователност, но не е постоянно. Възможна е многократна последователност на преминаване в зависимост от избраната начална и опорна точка на проучване.
Препоръчителни статии
Това е ръководство за алгоритма на DFS. Тук обсъждаме стъпка по стъпка обяснение, пресичаме графиката във формат на таблицата с предимства и недостатъци. Можете също да прегледате и другите ни свързани статии, за да научите повече -
- Какво е HDFS?
- Алгоритми за задълбочено обучение
- HDFS Команди
- SHA Алгоритъм