Пример за сложна лихва - Практически примери с формула

Въведение в пример за сложна лихва

Има достатъчно примери за сложен интерес. Следващият различен пример за сложна лихва дава разбиране за най-често срещания тип ситуации, при които сложната лихва се изчислява и как човек може да изчисли същото. Тъй като има множество области и ситуации, при които сложната лихва може да бъде изчислена, не е възможно да се предоставят всички видове примери. И така, някои от примерите за сложен интерес са дадени по-долу, показващи различните ситуации

Примери за сложен интерес (с шаблон на Excel)

Нека вземем пример, за да разберем по-добре изчислението на сложната лихва.

Можете да изтеглите този пример за сложна лихва Excel Шаблон тук - Пример за сложен интерес Пример за шаблон на Excel По-долу са примерите на сложния интерес:

Пример за съединена лихва -1

Хари иска да започне спестяванията от спечелените от него пари. След това той решава да внесе първоначалната сума от 10 000 долара в спестовната сметка с висока лихва. В този случай лихвеният процент ще бъде 15% годишно, като се умножава годишно. В момента възрастта на Хари е 40 години и той планира да се пенсионира на възраст 60 години. Това означава, че Хари има времевия хоризонт от 40 години, за да може да натрупа лихвата. Изчислете сумата пари, която Хари ще получи на възраст 60 години. Също така, подгответе таблицата, за да покажете годишната лихва и стойността на сметката.

Като се има предвид,

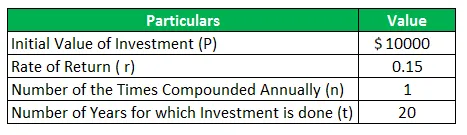
Решение:

Използвайки предоставената информация, изчисляването на сложната лихва и сумата, която трябва да бъде получена на възраст 60 години, е както следва:

Изчисляването на бъдещата стойност на инвестицията, използвайки формулата на сложната лихва, е както следва:

A = P (1 + r / n) ^nt

A = 10 000 $ (1 + 0, 15 / 1) ^{1 * 20}
A = 10 000 $ (1 + 0, 15) ²⁰
A = 10 000 долара (1, 15) ²⁰
A = 10 000 $ * 16, 367
A = 163 665, 37 $

Таблица за показване на годишната лихва и стойността на сметката

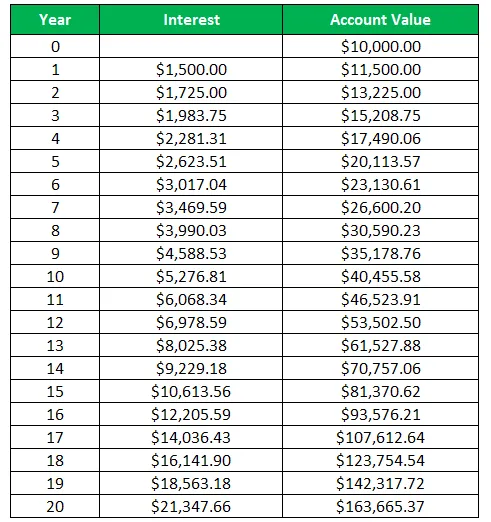
Тук лихвата се изчислява като:

Лихва = Начална сума на инвестицията * Лихвен процент (r)
Лихва = 10000 * 15%
Лихва = 1500 долара

По същия начин за всички години.

и стойността на акаунта се изчислява като:

Стойност на сметката = Начална сума на инвестиция + лихва
Стойност на сметката = 10000 + 1500
Стойност на акаунта = $ 11500

По същия начин за всички години.

В настоящия пример можем да видим, че стойността на сметката на инвестицията, направена първоначално от 10 000 долара, става 163 665, 37 долара в края на 20-годишния период. Това подчертава силата на съставянето, тъй като с помощта на сложни лихви Хари умножи парите си до многократно, без да управлява инвестицията активно. Тук Хари успя да спечели лихвата и върху спечелената по-рано лихва.

Пример за сложна лихва -2

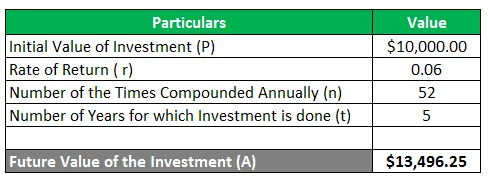
Сам прави първоначална инвестиция от 10 000 долара за период от 5 години. Той иска да знае размера на инвестицията, която ще получи след 5-те години, ако инвестицията спечели възвръщаемостта от 6% годишно, съставена седмично.

Като се има предвид,

Използвайки предоставената информация, изчисляването на сложната лихва и сумата, която трябва да бъде получена след периода от 5 години, е както следва:

Решение:

Изчисляването на бъдещата стойност на инвестицията чрез формула за сложна лихва е по-долу:

A = P (1 + r / n) ^nt

A = 10 000 $ (1 + 0, 6 / 52) ^{52 * 5}

A = 10 000 $ (1 + 0, 00115) ²⁶⁰

A = 10 000 долара (1.00115) ²⁶⁰

A = $ 10 000 * 1.3496

A = 13 496, 25 $

В настоящия пример можем да видим, че стойността на сметката на инвестицията, направена първоначално от 10 000 долара, става 13 496, 25 долара в края на 5-годишния период, когато комбинирането се извършва седмично. Съставянето увеличава стойността на инвестицията в края на периода, тъй като лихвата се печели и по-рано спечелената лихва. Тук съставянето се прави 52 пъти, тъй като има 52 седмици в годината.

Заключение - Пример за сложна лихва

Сложната лихва дава по-голям лихвен процент в сравнение с обикновената лихва, тъй като се получава чрез начисляване на лихва върху непогасена главница, включително лихва за разлика от обикновената лихва, когато лихвата се начислява върху първоначалната сума на главницата и не се начислява лихва над лихва. Силата на съставянето помага за увеличаване на инвестицията с по-голяма скорост, притежаваща характеристиките на експоненциалната функция. Резултатът е от факта, че въпреки изплащането на инвестицията, те се реинвестират, за да растат по-бързо. Това често се използва в нормалните бизнес практики, било то в случай на заем или депозит. Освен това, колко често се прави състава, също ще бъде решаващ фактор за растежа. Да предположим, че при някаква норма честотата на съставяне е на месец, тогава нейната годишна норма ще бъде повече от честотата на съставяне полугодишно или годишно.

Препоръчителни статии

Това е ръководство за примера на сложния интерес. Тук обсъждаме как да изчислим сложната лихва, използвайки нейната формула заедно с практически примери. Може да разгледате и следните статии, за да научите повече -