
Формулирана формула за годишен темп на растеж (Съдържание)
- формула
- Примери
- калкулатор
Каква е формулираната формула на годишния темп на растеж?
Усложняването е ефектът, при който инвестицията печели лихва не само върху основния компонент, но и дава лихва върху лихвата. Така сложният годишен темп на растеж е ефективният годишен ръст, спечелен от инвестициите, като се има предвид комбинирането в картината. Това основно предполага, че лихвата, спечелена всяка година, се реинвестира и печели същата лихва като основната сума. Това е причината, че сложният годишен ръст винаги е по-висок от обикновения лихвен процент. Много инвестиции като взаимни фондове, възвръщаемостта на фондовите борси не са много линейни и по много нестабилен начин.
Смесеният годишен темп на растеж помага за изглаждането на тази възвръщаемост и ще покаже колко инвеститор е спечелил през срока на инвестицията, като се има предвид факта, че всички печалби между този период се реинвестират със същия темп. Поради този ефект на изглаждане, той ни помага да сравняваме набори от данни с различно ниво на променливост. Много често се използва за целите на финансовия анализ.
Крайна сума на инвестицията = Начална сума (1 + CAGR) Брой години
Формулата за съставен годишен темп на растеж -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Тази формула е приложима, ако инвестицията се усложнява ежегодно, означава, че реинвестираме парите на годишна база. Но понякога се случва, че искаме да изчислим скоростта, в която смесването се случва на тримесечна, месечна, ежедневна база. За това използваме формулата по-долу:
Крайна сума на инвестицията = Начална сума (1 + CAGR / Усложняваща честота) (Брой години * Сложна честота)
И така, формула за съставен годишен темп на растеж -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Сложна честота:
- Полумесечно сглобяване: 2
- Тримесечно съставяне: 4
- Месечна честота: 12 и т.н.
Примери за формула на CAGR (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на формулата на CAGR.
Можете да изтеглите този сложен шаблон на Excel за годишен темп на растеж тук - Сложен шаблон за годишен темп на растеж в ExcelCAGR Формула - Пример №1
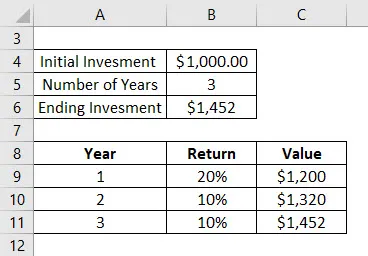
Да речем, че сте инвестирали 1000 долара във взаимни фондове преди 3 години. Следва връщането, което сте получили за тези 3 години:
- 1- ва година имате 20% увеличение на стойността. Така общата стойност е 1200 долара в края на 1- ва година
- На 2- ра година вие получихте 10% увеличение на стойността. Така общата стойност е $ 1320 в края на 2- ра година
- 3 -та година, вие получихте 10% увеличение на стойността. Така че общата стойност е $ 1452 в края на третата година
CAGR се изчислява по формулата, дадена по-долу
CAGR = (Крайна сума на инвестицията / Начална сума) (1 / Брой години) - 1
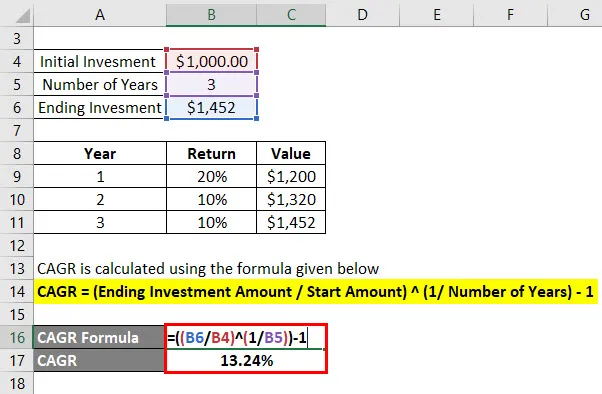
- CAGR = (1, 452 $ / 1000 $) (1/3) - 1
- CAGR = 13, 24%
Тук можем да видим, че годишната възвръщаемост за всичките 3 години е различна и варира, но сложният годишен темп на растеж ни дава единна ставка, която можем да сравним с различни възможности за инвестиции.
CAGR Формула - Пример №2
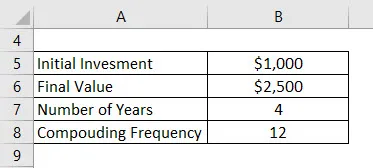
Да речем, че сте инвестирали 1000 долара в банката и искате да запазите парите в банката за 4 години. Нека сега да кажем, че общата сума, която получавате след 4 години, е 2500 долара. Банка предлага лихвен процент с месечни смеси. Изчислете CAGR.
CAGR се изчислява по формулата, дадена по-долу
CAGR = Усложняваща честота * ((Крайна сума на инвестицията / Начална сума) (1 / (Брой години * Сложна честота)) - 1)
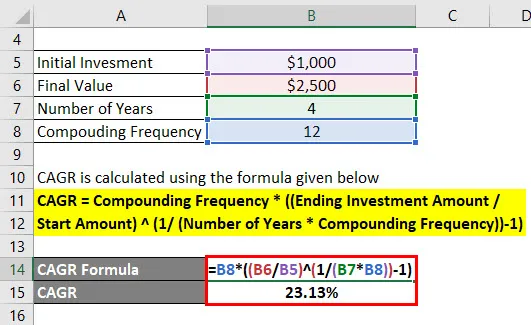
- CAGR = 12 * ((2500 $ / 1000 $) (1 / (4 * 12)) - 1)
- CAGR = 23.13%
Така сложният годишен темп на растеж е 23, 13%.
Обяснение на формулата за съставен годишен темп на растеж
Въпреки че съставният годишен темп на растеж е годишният темп на инвестицията, той е само теоретична цифра и не е истинската възвръщаемост. Основното предположение тук е, че всички печалби се реинвестират със същия процент за инвестиционния период, но курсът няма да остане за всички години и може да не инвестираме парите си със същия процент. Така че това е единствената представителна ставка, която ни казва, че това, което бихме могли да свършим, ако всички пари се реинвестират в края на всяка година по този курс. Така че има някои основни моменти, които трябва да вземем предвид, когато използваме сложен годишен темп на растеж.
Също така, ние ще бъдем много внимателни за инвестиция, която е дълъг период. Например, ако инвестиционният период е много дълъг, да речем 20 години, комбинираният годишен лихвен процент може да ни даде грешна индикация, защото може да се случи, че не печелим печалба през първите 15 години, а всички възвръщаемости идват през последния период, Печеленето на печалба за 15 години не е приемливо за всеки бизнес да поддържа.
По същия начин, ако две възможности за инвестиции имат един и същ CAGR, може да се окаже, че единият е по-привлечен от другия поради причината, че растежът при едното се случва в началния период, докато при други, той е концентриран в края на месечен цикъл.
Съответствие и употреба на формулата за съставен годишен темп на растеж
Съставният годишен темп на растеж наистина е полезен при изчисляването на средния темп на растеж на инвестицията и може да помогне при сравняването на различни инвестиции. Както видяхме в горния пример, ръстът на инвестициите от година на година е неравномерен и нередовен. Но използвайки сложен годишен темп на растеж, възвръщаемостта изглажда. Друг фактор, който прави съставеният годишен темп на растеж критичен метод за определяне на растежа на инвестицията, е, че той взема предвид ефекта на комбиниране, който годишната възвръщаемост не прави. Смесеният годишен лихвен процент не ни дава реалната картина на възвръщаемостта, тъй като той само изчислява възвръщаемостта на основната сума и игнорира лихвата по лихвения компонент, но това не е така при сложния годишен темп на растеж.
Съставен калкулатор на формула за годишен темп на растеж
Можете да използвате следния съставен калкулатор за годишен растеж
| Крайна сума на инвестицията | |
| Начална сума | |
| Брой години | |
| CAGR | |
| CAGR = | ((Крайна сума на инвестицията / Начална сума) 1 / Брой години -1 |
| = | ((0/0) 1/0 -1) = 0 |
Препоръчителни статии
Това е ръководство за формулата за съставен годишен темп на растеж. Тук обсъждаме как да изчислим CAGR заедно с практически примери. Ние също така предлагаме сложен калкулатор на годишния темп на растеж с възможност за сваляне на шаблон Excel. Можете също да разгледате следните статии, за да научите повече -
- Ръководство за формула на норма на възвръщаемост
- Примери за формула на експоненциален растеж
- Калкулатор за формула на теоремата за централен лимит
- Как да изчислим пазарната капитализация?