Разлика между линейна регресия срещу логистична регресия
Следващата статия Линейна регресия срещу логистична регресия предоставя най-важните разлики между двете, но преди да разберем какво означава регресията?
регресия
Регресията е основно статистическа мярка за определяне на силата на връзката между една зависима променлива, т.е. продукцията Y и поредица от други независими променливи, т.е. X 1, X 2 и така нататък. Регресионният анализ се използва основно за прогнозиране и прогнозиране.
Какво е линейна регресия?
Линейната регресия е алгоритъм, който се основава на контролираната учебна област на машинно обучение. Той наследява линейна връзка между входните променливи и единичната променлива променлива, където изходната променлива е непрекъсната по своя характер. Използва се за прогнозиране на стойността на продукцията, да кажем Y от входовете, да кажем X. Когато се счита само за един вход, той се нарича проста линейна регресия.
Може да се класифицира в две основни категории:
1. Проста регресия
Принцип на действие: Основната цел е да се намери уравнението на права линия, която най-добре пасва на извадените данни. Това уравнение алгебрично описва връзката между двете променливи. Най-подходящата права линия се нарича регресионна линия.
Y = β 0 + β 1 X
Където,
β представлява характеристиките
β 0 представлява прихващането
β 1 представлява коефициентът на характеристика X
2. Многомерна регресия
Използва се за прогнозиране на корелация между повече от една независима променлива и една зависима променлива. Регресията с повече от две независими променливи се основава на прилягащата форма към съзвездието от данни на многоизмерна графика. Формата на регресия трябва да бъде такава, че да минимизира разстоянието на формата от всяка точка на данните.
Моделът на линейни отношения може да бъде представен математически, както е показано по-долу:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Където,
β представлява характеристиките
β 0 представлява прихващането
β 1 представлява коефициентът на характеристика X1
β n представлява коефициентът на характеристиката X n
Предимства и недостатъци на линейна регресия
По-долу са дадени предимства и недостатъци:
Предимства
- Поради своята простота, той се използва широко моделиране за прогнози и изводи.
- Тя се фокусира върху анализа на данните и предварителната обработка на данните. Така че, той се занимава с различни данни, без да се занимава с детайлите на модела.
Недостатъци
- Работи ефективно, когато данните се разпространяват нормално. По този начин за ефективно моделиране трябва да се избягва колинеарността.
Какво е логистична регресия?
Това е форма на регресия, която позволява прогнозиране на дискретни променливи чрез смесване на непрекъснати и дискретни предиктори. Това води до уникална трансформация на зависими променливи, която влияе не само върху процеса на оценка, но и на коефициентите на независими променливи. Той адресира същия въпрос, който прави множествената регресия, но без предположения за разпределение на прогнозите. При логистична регресия променливата на резултата е двоична. Целта на анализа е да се оцени ефекта на множество обяснителни променливи, които могат да бъдат числови или категорични или и двете.
Видове логистична регресия
По-долу са описани 2 вида логистична регресия:
1. Двоична логистична регресия
Използва се, когато зависимата променлива е дихотомична, т.е. като дърво с два клона. Използва се, когато зависимата променлива е непараметрична.
Използва се, когато
- Ако няма линейност
- Има само две нива на зависимата променлива.
- Ако многомерната нормалност е съмнителна.
2. Мултиномиална логистична регресия
Мултиномиалният логистичен регресионен анализ изисква независимите променливи да са метрични или дихотомични. То не прави никакви предположения за линейност, нормалност и хомогенност на дисперсията за независимите променливи.
Използва се, когато зависимата променлива има повече от две категории. Използва се за анализ на връзки между неметрична зависима променлива и метрични или дихотомични независими променливи, след което сравнява множество групи чрез комбинация от бинарни логистични регресии. В крайна сметка тя предоставя набор от коефициенти за всяко от двете сравнения. Коефициентите за референтната група се приемат като всички нули. И накрая, прогнозирането се прави въз основа на най-високата резултатна вероятност.
Предимство на логистичната регресия: Това е много ефективна и широко използвана техника, тъй като не изисква много изчислителни ресурси и не изисква никаква настройка.
Недостатък на логистичната регресия: Не може да се използва за решаване на нелинейни проблеми.
Сравнение между главата между линейна регресия и логистична регресия (Инфографика)
По-долу са топ 6 разликите между линейна регресия срещу логистична регресия 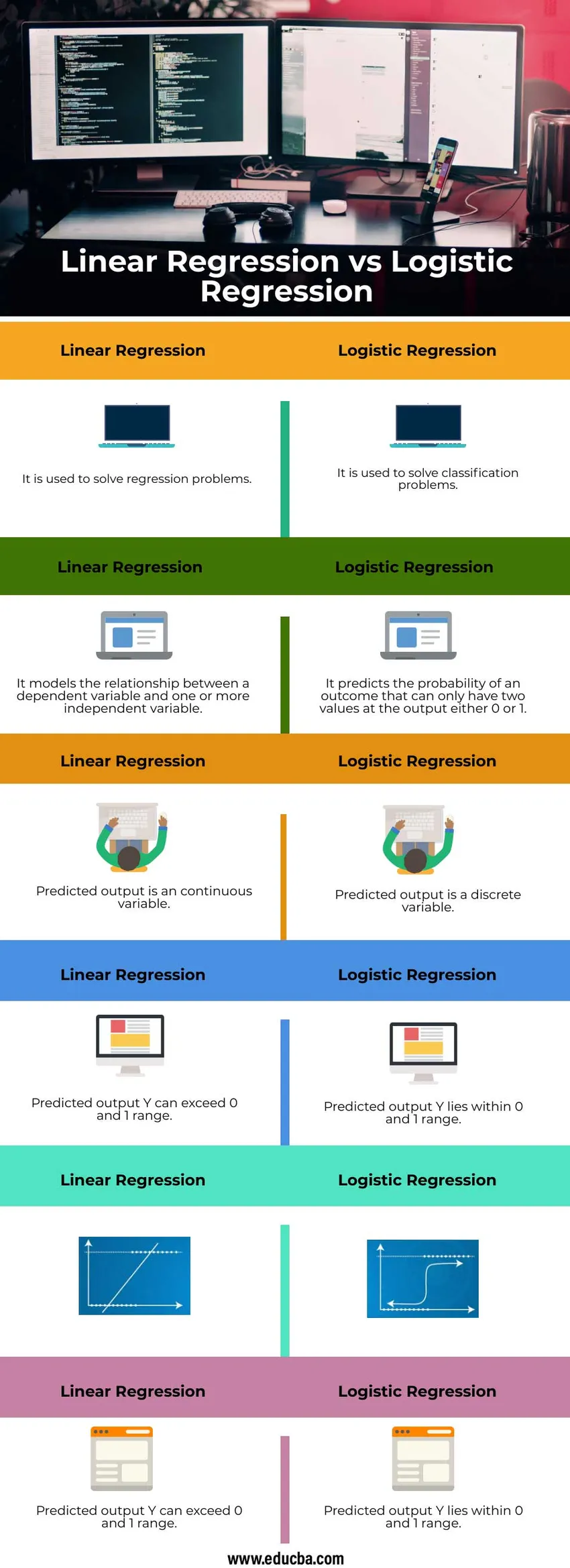
Ключова разлика между линейна регресия срещу логистична регресия
Нека обсъдим някои от основните ключови разлики между линейна регресия срещу логистична регресия
Линейна регресия
- Това е линеен подход
- Използва права линия
- Не може да приема категорични променливи
- Той трябва да игнорира наблюдения с липсващи стойности на числовата независима променлива
- Изходът Y е даден като
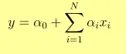
- 1 единично увеличение на x увеличава Y с α
Приложения
- Предсказване на цената на даден продукт
- Прогнозиране на резултат в мач
Логистична регресия
- Това е статистически подход
- Използва сигмоидна функция
- Може да приема категорични променливи
- Той може да взема решения, дори ако има наблюдения с липсващи стойности
- Изходът Y е даден като, където z е дадено като
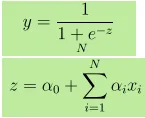
- 1 единично увеличение на x увеличава Y с коефициент на лога на α
- Ако P е вероятността за събитие, тогава (1-P) е вероятността тя да не се случи. Коефициент за успех = P / 1-P
Приложения
- Прогнози дали днес ще вали или не.
- Предсказване дали имейл е спам или не.
Таблица за линейна регресия срещу логистична регресия
Нека обсъдим топ сравнение между линейна регресия срещу логистична регресия
|
Линейна регресия |
Логистична регресия |
| Използва се за решаване на проблеми с регресията | Използва се за решаване на проблеми с класификацията |
| Той моделира връзката между зависима променлива и една или повече независима променлива | Той прогнозира вероятността от резултат, който може да има само две стойности на изхода или 0 или 1 |
| Прогнозираният изход е непрекъсната променлива | Предсказаният изход е дискретна променлива |
| Прогнозираният изход Y може да надвишава 0 и 1 обхват | Прогнозираният изход Y се намира в границите 0 и 1 |
 | 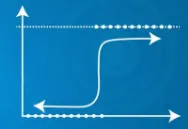 |
| Прогнозираният изход Y може да надвишава 0 и 1 обхват | Прогнозиран изход |
заключение
Ако функциите не допринасят за прогнозиране или ако са в голяма степен свързани помежду си, това добавя шум към модела. Така че, функции, които не допринасят достатъчно за модела, трябва да бъдат премахнати. Ако независимите променливи са силно свързани, това може да причини проблем с мултиколинеарност, който може да бъде решен чрез пускане на отделни модели с всяка независима променлива.
Препоръчителни статии
Това е ръководство за линейна регресия срещу логистична регресия. Тук обсъждаме ключовите разлики между линейната регресия и логистичната регресия с инфографиката и таблицата за сравнение. Можете също така да разгледате следните статии, за да научите повече -
- Data Science срещу визуализация на данни
- Машинно обучение срещу невронна мрежа
- Контролирано обучение срещу задълбочено обучение
- Логистична регресия в R