Формула за ефективна годишна ставка (Съдържание)
- формула
- Примери
- калкулатор
Каква е формулата за ефективна годишна ставка?
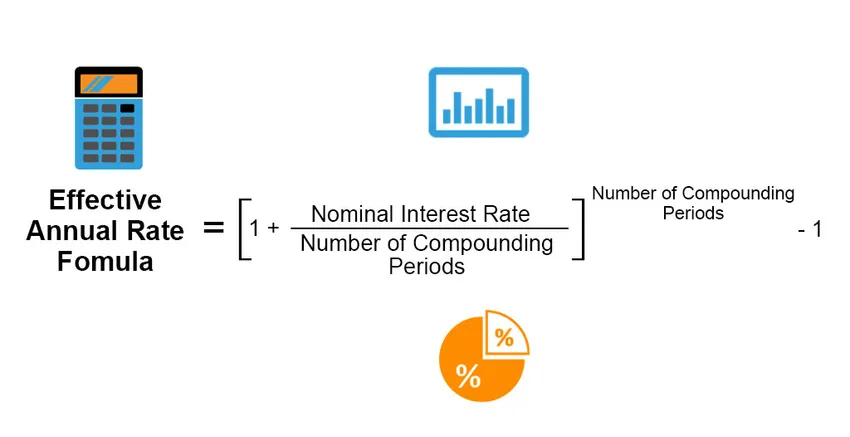
Ефективният годишен лихвен процент е действителният лихвен процент, който се печели или изплаща върху инвестиция, заем или друг подобен финансов продукт, и в противен случай е различен от „номиналния лихвен процент“ поради периода на изплащане на лихвата, съставен от лихвения процент, общ времеви период на заема или инвестицията и др. Ефективният годишен курс се изчислява по следната формула;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Примери за формула за ефективна годишна ставка (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на ефективната годишна ставка.
Можете да изтеглите този шаблон на формула за ефективен годишен курс формула тук - шаблон на формула за ефективен годишен курс ExcelФормула за ефективна годишна ставка - Пример №1
Да предположим, че г-н X взема личен кредит от банка с лихва от 20%, усложнена полугодишно. Изчислете ефективната годишна ставка, като използвате информацията.

Решение:
Ефективната годишна ставка се изчислява по формулата, дадена по-долу
Ефективна годишна ставка = ((1 + (Номинална лихва / Брой на периодите на усложняване)) Брой на периодите на усложняване) - 1

- Ефективна годишна ставка = ((1 + (20% / 2)) 2) - 1
- Ефективна годишна ставка = 21%
Формула за ефективна годишна ставка - Пример №2
Да предположим, че г-н А инвестира 100 долара в депозитен сертификат, който изплаща номинална годишна лихва от 10%, усложнена на тримесечна база. Изчислете ефективната годишна ставка.

Решение:
Ефективната годишна ставка се изчислява по формулата, дадена по-долу
Ефективна годишна ставка = ((1 + (Номинална лихва / Брой на периодите на усложняване)) Брой на периодите на усложняване) - 1
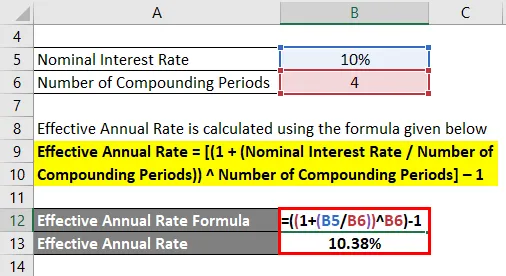
- Ефективна годишна ставка = ((1 + (10% / 4)) 4) - 1
- Ефективна годишна ставка = 10, 38%
Формула за ефективна годишна ставка - Пример №3
Нека приемем, че инвестициите във взаимни фондове получават 15, 50% годишна лихва като печалба, докато P2P Кредитът печели 15% годишен номинален лихвен процент, усложнен месечно. Затова изчислете ефективната годишна ставка и за двата случая.

Решение:
Ефективната годишна ставка се изчислява по формулата, дадена по-долу
Ефективна годишна ставка = ((1 + (Номинална лихва / Брой на периодите на усложняване)) Брой на периодите на усложняване) - 1
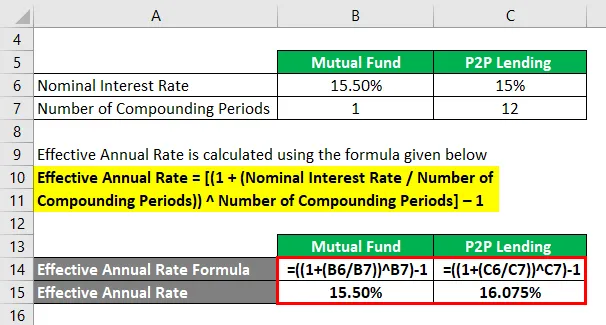
За взаимен фонд
- Ефективна годишна ставка = ((1 + (15.50% / 1)) 1) - 1
- Ефективна годишна ставка = 15, 50%
За P2P кредитиране
- Ефективна годишна ставка = ((1 + (15% / 12)) 12) - 1
- Ефективна годишна ставка = 16.075%
обяснение
Номиналният лихвен процент е посоченият процент върху финансовия продукт. В Пример 3, номиналният лихвен процент, показан върху продуктите, прави Взаимния фонд да изглежда като предпочитан избор на инвестиция за инвеститорите поради 0, 50% по-висок годишен номинален лихвен процент.
Ефективният годишен лихвен процент обаче се изчислява, като се вземе номиналният годишен лихвен процент и се смеси за броя на посочените периоди (12, ако събирането е месечно; 6, ако събирането е двумесечно; 4, ако е тримесечно; и 2, ако е е полугодишно), приложимо за период от една година. В случай на взаимен фонд, броят на периодите на запълване на година е 1, докато в случай на P2P заемане е месечно обединяване, следователно има 12 периоди на събиране.
Въз основа на формулата,
Ефективни годишни възвръщаемости = ((1 + (номинален лихвен процент / брой периоди на запълване)) (брой на периодите на съставяне) - 1
Ефективна годишна възвръщаемост на взаимния фонд = ((1 + (15.50% / 1)) 1) - 1 = 15.50%
Ефективна годишна възвръщаемост на заем P2P = ((1 + (15.00% / 12)) 12) - 1 = 16.075%
Уместност и използване на формулата за ефективна годишна ставка
Формулата на ефективния годишен лихвен процент се използва за разграничаване на действителната IRR (вътрешна норма на възвръщаемост) или годишна доходност за лихвен процент, който може или не може да се комбинира многократно за даден период. Това би могло да се използва много добре при сравняване на различни видове възможности за инвестиции или заеми, взети под различни структури.
Нека приемем, че има 2 възможности за инвестиция, срочни депозити в пощенски офис и банкови фиксирани депозити, до които инвеститорът се е стеснил, като се има предвид неговият риск и пригодност за риск. Крайната цел на инвеститора е да извлече максимума от тези депозити и да спечели по-висока доходност. И двата инструмента обаче предлагат малко по-различни лихвени проценти, докато срочният депозит на пощенските станции предлага тримесечни усложнения за разглеждания срок.
- Сума на инвестицията: Rs. 10 lakhs
- Период на инвестиране: 5 години
- Банков фиксиран депозит: 7, 5% годишна лихва
- Срочен депозит след пощенски офис: 7.4% годишна лихва, усложнена тримесечно
По отношение на предлаганите годишни лихвени проценти изглежда, че Банковият депозит е по-добрият вариант. Въпреки това, ако инвеститорът действително изчисли коефициента на тримесечно усложняване на срочния депозит на пощенския офис, това води до ефективна годишна ставка / възвръщаемост от 7, 61%.
Поради тази малка промяна от 7.4% на 7.61% в ефективна ставка, инвеститорът ще спечели общо Rs. 4, 42, 848.28 от този конкретен инструмент, докато той / тя би спечелил Rs. 3, 35, 469.14 от инструмента за банков депозит.
Ако инвеститорът пропусне изчисляването на тази ефективна годишна ставка, той / тя би загубил възможността да спечели приблизително повече от Rs. 1 лек от неговата инвестиция.
Калкулатор на формула за ефективна годишна ставка
Можете да използвате следния калкулатор на ефективната годишна ставка
| Номинална лихва | |
| Брой на сложните периоди | |
| Ефективна годишна ставка | |
| Ефективна годишна ставка = | ((1 + (Номинален лихвен процент / Брой на периодите на усложняване)) Брой периоди на усложняване ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Препоръчителни статии
Това е ръководство за формулата за ефективна годишна ставка. Тук обсъждаме как да изчислим ефективната годишна ставка заедно с практически примери. Ние също така предлагаме ефективна годишна ставка калкулатор с изтеглящ се шаблон Excel. Можете също да разгледате следните статии, за да научите повече -
- Калкулатор за формула за реален лихвен процент
- Формула за възвръщаемост на заетия капитал | дефиниция
- Как да изчислим ефективната лихва?
- Каква е настоящата стойност на формулата за анюитет?