Въведение в сортирането на купчината в С
Сортирането е техника, която се отнася до подреждането на елементи въз основа на различни свойства. (Свойства като подреждане на данни във възходящ, низходящ или азбучен ред). Един основен пример за сортиране, за който можем да мислим тук, е подреждането на артикули по време на онлайн пазаруване. Можем да се свържем с цени, популярност, най-новите и така нататък. Така че има много техники за това позициониране на елементи чрез сортиране. В тази тема ще научим за сортирането на Heap в C.
Тук ще научим една от най-разпространените техники за сортиране, Heap Sort, чрез език за програмиране на C.
Логиката за Heap Sort
Как всъщност можем да извършваме сортиране на купчина? Нека да проверим по-долу.
Първо, купчината е една от структурата на данните на базата на дърво. Дървото, участващо тук, винаги е цялостно бинарно дърво. И има два вида грамада
- Min - Heap: Обикновено подредени във възходящ ред, тоест ако елементът на родителския възел има стойност, по-малка от тази на дъщерните елементи на възела.
- Max - Heap: Обикновено подредени в низходящ ред, тоест ако елементът на родителския възел има стойност, по-голяма от тази на дъщерните елементи на възела.
Стъпки за сортиране на купчина
- След като се получат несортирани данни от списъка, елементите се организират в структурата на данните за купчината или въз основа на създаване на min-heap или max-heap.
- Първият елемент от горния списък се добавя в нашия масив
- Отново се формира техниката на структурата на данните на главата, същата като първата стъпка, и отново или най-високият елемент, или най-малкият елемент се прибира и добавя в нашия масив.
- Повторните стъпки ни помагат да получим масива със сортиран списък.
Програма за сортиране на купчина в С
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Първо, ние молим потребителя да въведе броя на елементите, които са взети за сортиране, а след това на потребителя е разрешено да въведе различни елементи, които трябва да бъдат сортирани.
Следващи стъпки
- Следващото, върху което се фокусираме, е да създадем масив от хепа, в този случай - макс.
- Основното условие за получаване на max - heap масив е да се провери дали никоя стойност на родителския възел не е по-малка от стойността му на дъщерния възел. Ще разменяме, докато постигнем това условие.
- Основното предимство в това пълно двоично дърво е, че левите и десните възли на родителския възел могат да бъдат достъпни със стойности 2 (i) + 1 и 2 * (i) + 2 съответно. Където аз съм родителският възел.
- Така че по този начин тук поставяме нашия корен възел, който съдържа максималната стойност в най-дясното място на листния възел. И след това отново следвайки същата процедура, така че следващият максимален брой сега се превръща в коренния възел.
- Ще следваме същата процедура, докато само един възел не остане в масива от купища.
- И тогава ние подреждаме нашия масив от масиви, за да образуваме перфектен сортиран масив в увеличаващ се ред.
- Накрая отпечатваме сортирания масив в изхода.
изход:
Изходът е приложен по-долу.
Нека ви покажа изобразителното представяне на събитията:
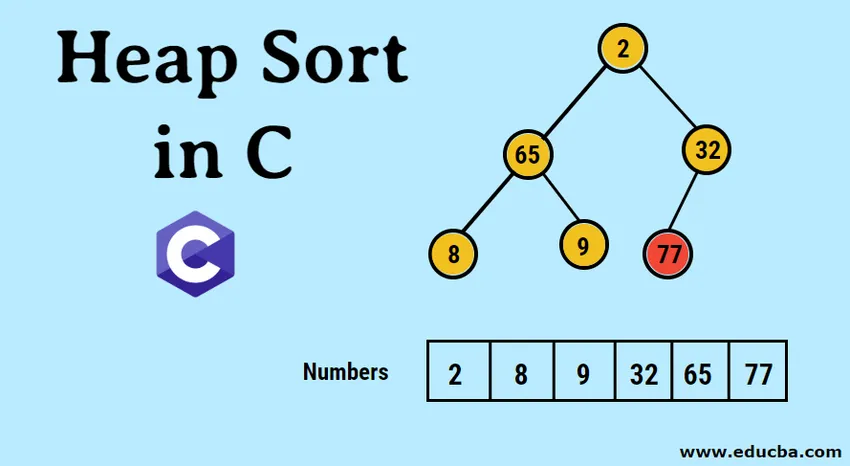
- Въведените данни първо се представят под формата на едномерен масив, както следва.

- Изобразителното изображение на образуваното бинарно дърво е, както следва:
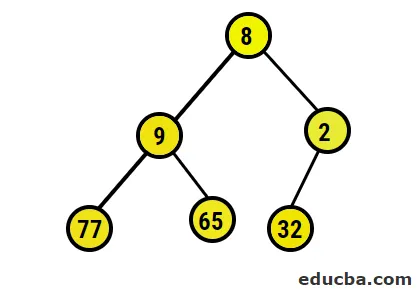
- Сега ние ще преобразуваме в max heap, като се уверим, че всички родителски възли са винаги по-големи от дочерните възли. Както беше споменато в изхода под масив, сортиран с масив, изобразителното представяне ще бъде:
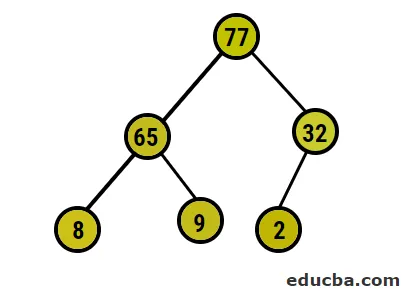
- След това ще заменим коренния възел с крайния листен възел и след това ще го изтрием от дървото. Листовият възел ще бъде коренът сега и отново същия процес e последван, за да получи отново най-високия елемент в корена
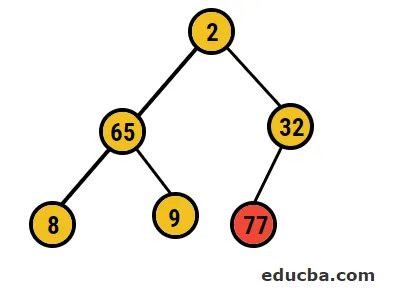
- Така че в този случай 77 цифри се изтриват от това дърво и се поставят в нашия сортиран масив и процесът се повтаря.
По-горе сме го виждали за формиране на максимален масив. Същият процес се разглежда и с образуването на масив от мин. Купчина. Както беше обсъдено по-горе, единствената разлика е във връзката между елементите на родителя и дъщерния възел.
Като упражнение можете ли да опитате да формирате сорта на купчината в низходящ ред?
заключение
Въпреки че има много техники за сортиране, сортирането на купчината се счита за една от най-добрите техники за сортиране поради сложността й във времето и пространството. Сложността на времето за всички най-добър, среден и най-лош случай е O (nlogn), където сложността в най-лошия случай е по-добра от сложността на най-лошия случай на Quicksort, а пространствената сложност е O (1).
Препоръчителни статии
Това е ръководство за сортирането на Heap C. Може да разгледате и следните статии, за да научите повече -
- Сортиране в купа с Java
- Сортиране на селекцията в Java
- Палиндром в програма C
- Модели в C програмирането
- Сортиране на купчина в C ++ (Алгоритъм)
- Сортиране на купи в Python
- C Матрично умножение на програмиране