
Excel SIN функция (Съдържание)
- SIN функция в Excel
- Как да използвам функцията SIN в Excel?
SIN функция в Excel
Да можеш да изчислиш, не обхваща цялата математика. Това е негов подраздел, макар и жизненоважен за неговото приложение. В миналите години това беше ограничаващият фактор, с изключение на много известните и изключително талантливи „човешки калкулатори“, като Шакунтала Деви. Но компютрите сега ви позволяват да направите цялата математика по-интелектуална. Концепциите и теоремите на математиката са по-значими сега от всякога.
Excel е много умел в работата с множество математически модели, въоръжен е с богата колекция от математически и логически функции за подпомагане на различни операции. Той предоставя цял набор от тригонометрични функции, за да ни помогне, когато се натъкнем на света на тригонометрията.
И така, за да се реши тригонометричната функция Sine, тя осигурява функцията SIN . Това е основна тригонометрична функция, но е удобно, особено ако работите в производството, навигацията или комуникациите. Но е важно да се отбележи, че Excel използва радиани, а не градуси, за да изчисли каквото и да е тригонометрично изражение. Има два начина за това:
- Спомнете си, че π = 180 °. Така че, ако ъгълът е в градуси, умножете го с π / 180 °, за да го преобразувате в радиани. В Excel това преобразуване може да бъде написано PI () / 180. Например, за да преобразувате 60 ° в радиани, изразът на Excel би бил 60 * PI () / 180, което е равно на 1.0472 радиана.
- Excel е оборудван и с много полезен инструмент, често наричан RADIANS. Той приема ъгъл като аргумент, при който ъгълът се отнася до градусите, които трябва да бъдат превърнати в радиани. Вземете пример, когато изразът, който се използва за преобразуване на 210 ° в радиани, е „RADIANS (210)“ и оценява на 66519 радиана.
И обратно, полезната програма DEGREES е еднакво важна. Тази функция може да се използва за точно обратното на функцията RADIANS чрез преобразуване на радиани в градуси. Например DEGREES (PI () / 2) оценява 90.
Как да използвам функцията SIN в Excel?
Нека разберем как да използваме SIN функцията в Excel, като използваме някои примери и реални илюстрации на SIN функцията в Excel.
Можете да изтеглите този шаблон за SIN функция за Excel тук - шаблон за функция SIN ExcelSIN функция в Excel - пример №1
Изчисляване на стойността на синуса с помощта на SIN функция в Excel
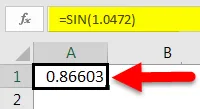
За да намерим синуса на определено число, първо трябва да напишем = SIN () в определена клетка.

Както можете да видите от горния екран, функцията SIN в Excel очаква число като вход. Това число обикновено представлява стойност в радиани.
Така че в този случай ще напишем „= SIN (1.0472)“, където 1.0472 е радианите, еквивалентни на 60 градуса.
След като направим това, ще получим стойността на SIN от 60 градуса.
SIN функция в Excel - пример №2
Изчисляване на стойността на синуса с помощта на SIN и RADIAN функция в Excel
Сега нека да видим как можем да използваме SIN по-продуктивен начин, в случай че не знаем точната стойност на радиан за степен.
Ще използваме RADIANS (), за да разберем стойността на радиан, която ще предадем като аргумент на функцията SIN.
И така, започваме с по-ранната версия на SIN ():

След това ще предадем RADIANS (60) като аргумент на функцията SIN, където 60 е стойността в градуси.

Както можем да видим от примера по-горе, RADIANS () приема стойност в градуси. Така че, ние ще предадем 60 като стойност на RADIANS ().

След това натиснете Enter. Това дава следния резултат.

И така, виждаме, че резултатът е същият като първия пример.
SIN функция в Excel - пример №3
Изчисляване на стойността на синуса с помощта на SIN и PI функция в Excel
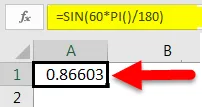
Има още един начин за преобразуване на степенна стойност в радиани за нашата употреба във функцията SIN. Спомняме си от времето в училище, че π = 180 °. Така че, ако ъгълът е в градуси, умножете го с π / 180 °, за да го преобразувате в радиани. В Excel това преобразуване може да бъде написано PI () / 180. Например, за да преобразувате 60 ° в радиани, изразът на Excel би бил 60 * PI () / 180, което е равно на 1.0472 радиана.
Нека да видим как работи това:
Започваме, като пишем функцията SIN по същия начин, както по-горе.

След това директно ще предадем 60 ° като аргумент на функцията SIN. Но това не би ни дало съответната стойност от 60 градуса в радиани. Следователно ще умножим 60 по PI () / 180.

Това ще ни даде следния резултат:
Както виждаме, това е същото като горните примери.
SIN функция в Excel - пример №4
Сега, нека да разгледаме друг пример, показващ резултатите от функцията SIN за различни стойности.

Обяснение на резултатите, показани в горната таблица:
Случай 1 и 2:
3.14 е стойността на Pi и можем да използваме и двата метода, за да получим стойност 0. Това основно означава, че SIN на Pi radians е 0 .
Дело 3 и 4:
Radians и Pi / 180 имат еднаква стойност в математиката и следователно функцията SIN дава една и съща стойност. И двата примера предполагат SIN от 30 градуса, което дава стойност 0, 5.
Дело 5 и 6:
SIN 45 = 0, 85 е SIN от 45 радиана, което означава, че по подразбиране excel поема всички ъгли в радиани, а не степен. За да го преобразуваме в степен, можем да използваме радиева функция и да получим SIN от 45 градуса, както е показано в последния ред. т.е. SIN (RADIANS (45)) = 0.707 или 0.71
SIN функция в Excel - пример №5
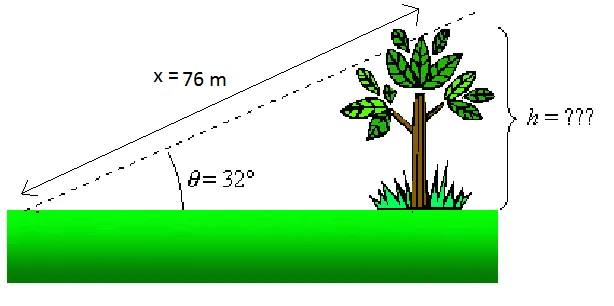
Кажете например, че искаме да знаем височината на дървото на фигурата, показана по-горе. Знаем, че ако застанем на 76 m от върха на дървото (x = 76 m), зрителната линия към върха на дървото е 32 ° по отношение на хоризонта (θ = 32 °). Ние знаем, че:
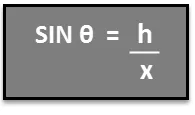
Следователно, за да решим за височината на дървото h, намираме h = x SIN θ.

Функцията SIN има само един аргумент, който е число. За изчисляването на SIN от него е необходимо число. Следователно е жизненоважно да се преобразуват градуси в число в радиани, преди да се намери синусът на него.
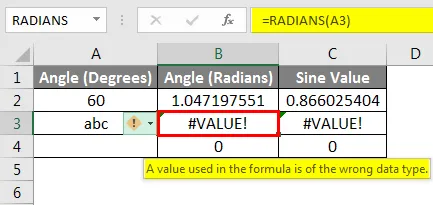
Функцията SIN показва #VALUE! грешка, ако препратката, използвана като аргумент на функцията, сочи към клетка, съдържаща текстови данни. В показания по-долу пример, използваната референция на клетката на третия ред сочи текстовия етикет в ъгъл (градуси) . Тъй като функциите SIN поддържат само число като аргумент, SIN ще оцени до грешка, в този случай, # VALUE!, Ако клетката сочи към празна клетка, функцията връща стойност нула, както е показано в примера по-долу. Тригонометричните функции на Excel тълкуват празните клетки като нула, а синусът на нулевите радиани е равен на нула.
SIN функция в Excel - пример №6
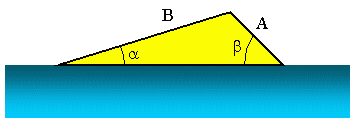
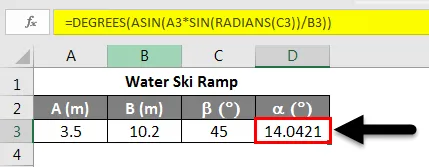
Нека предположим, че искаме да открием ъгъла на стартиране на рампа за водни ски, както е на фигурата по-горе. Знаем, че A = 3, 5 m, B = 10, 2 m и b = 45, 0 °. Сега, за да намерим a, можем да използваме Закона на синусите. В този сценарий може да се запише като:
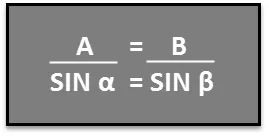
Можем да организираме това уравнение като:
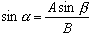
Използвайки дъговия или обратния синус, можем да открием ъгъла α . Прилагане на уравнението, показано по-долу.

Пример №7
В нашия последен тригонометричен пример ще използваме Excel за изследване на тригонометричната идентичност:
sin²θ + cos²θ = 1
Имайте предвид, че на екрана по-долу тази идентичност важи, когато θ е даден както в радиани, така и в градуси.

Обърнете внимание, че описанието на единицата за ъгъла θ е поставено в различни клетки от числата. Ако поставим числата и единиците в една и съща клетка, Excel няма да може да разграничи числото от текста и следователно няма да можем да препратим клетките за използване в уравнение и това ще доведе до #VALUE! грешка.
Неща, които трябва да запомните
- Имайте предвид, че функцията SIN в excel работи с Radian по подразбиране.
- Преобразувайте номера, както се изисква в Radian или градус, използвайки или функция RADIANS, или DEGREES.
- Можете да използвате PI () функция, за да получите точни резултати от функцията SIN, докато работите с π.
Препоръчителни статии
Това е ръководство за SIN функцията в Excel. Тук обсъдихме Как да използваме SIN функцията в Excel, заедно с практически примери и шаблон за Excel, който може да се сваля. Можете да разгледате и другите ни предложени статии -
- Важни функции на математиката в Excel (лесно)
- Ръководство за разделяне на формули в Excel
- Важни формули и функции на Advanced Excel
- Cheat Sheet на Excel Formulas