
Въведение в сериите на Фибоначи в Python
Серия Фибоначи в Python, това се означава като поредица от числа, където следващото число е сумата от настоящите две числа.
Например:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. така нататък
Така че тук 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 и т.н.
Разглеждайки горното, човек би имал определена представа за какво говорим.
Въпреки това, по отношение на математическото правило, то може да бъде записано като:

Където n-то число е сумата от броя на места (n-1) и (n-2). Що се отнася до реализацията на серията Фибоначи, може да има редица кодиращи езици, чрез които би могло да се направи.
Въпреки това, Python е широко използван език в днешно време. Нека да видим реализацията на серията Фибоначи чрез Python. Човек трябва да е наясно с основните изявления за кондициониране като цикъла, ако не, докато цикъл и т.н. в Python, преди да продължите тук. Ако не, би било чудесно, ако някой може да го преразгледа и след това да се заеме с идващото съдържание. Тук с демонстрационна цел използвам шпион, който е IDE за език за програмиране на python. Човек може да използва всички други IDE или Ipython преносими компютри, както и за изпълнение на програмите Python.
Серия на Фибоначи в Python
Нека да видим прилагането на числата и сериите на Фибоначи, като се имат предвид 1- ви два елемента на Фибоначи са 0 и 1:
Можете обаче да настроите функцията на Фибоначи според вашето изискване, но първо да видите основите и постепенно да преминете към други.
Python Code за намиране на n число на Фибоначи
Код 1:
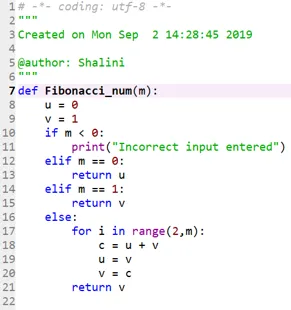
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Код 2:
изход:
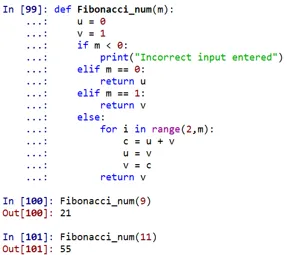
Както се вижда, числото на Фибоначи на 9 -о място би било 21, а на 11 -о място - 55.
- Тук „Weight_num“ е дефинирана функция, която се грижи за намирането на числото на Фибоначи с помощта на определени условия. Тази функция може да бъде извикана чрез посочване на всяка позиция.
Сега нека да видим как човек може да отпечата серии до споменатата позиция:
Код:
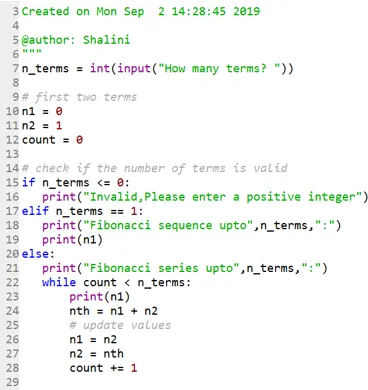
изход:
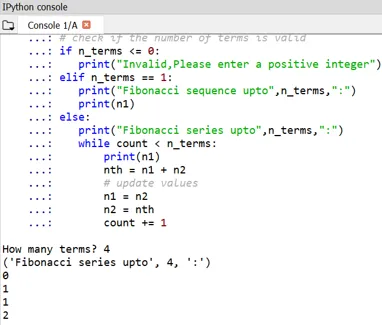
Може да се забележи, че началото на числата на Фибоначи е определено като 0 и 1.
- Ако някой иска да определи собствените си начални условия, това също може да стане по същия начин чрез настройване на n1 и n2. Ето примера за това:
Да кажем сега, че искаме нашите начални условия да бъдат: n1 = 3, n2 = 5
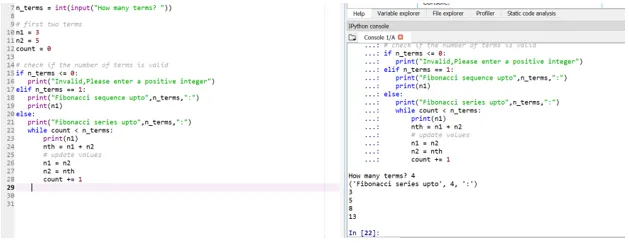
Така че тук вашата позиция на 4 -ти мандат (въвежда се потребителско въвеждане) ще бъде определена въз основа на началните ви условия.
Методи, чрез които могат да бъдат генерирани серии от Фибоначи
По-долу са трите метода, чрез които могат да бъдат генерирани серии от Фибоначи:
1. Чрез генератори
Код:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
изход:
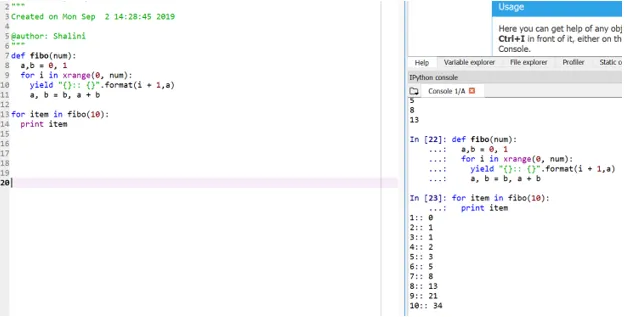
Този метод се нарича "генератор", тъй като функцията xrange е генератор на числата между 0 и число, а добивът е генераторът за форматиран изход.
Ето какво прави xrange за вас:

Тук сериите на Фибоначи са дефинирани под формата на функция, вътре в която за цикъл, xrange и функция за добив се грижи за изхода.
2. Чрез за контур
Код:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
изход:

Както се вижда, за отпечатването на сериите Фибоначи между 0 и 10. е използван прост за цикъл между 0 и 10. Вътре за цикъла на променливите са присвоени нови стойности. U и v са първоначалните стойности по подразбиране на Фибоначи, които са зададени съответно на 0 и 1.
Що се отнася до прогресирането на цикъла, новата стойност на u е старата стойност на v, докато новата стойност на v е сумата на старите стойности на u и v. Това продължава до края на стойностите на диапазона.
3. Чрез рекурсия
Код:
#Through recursion
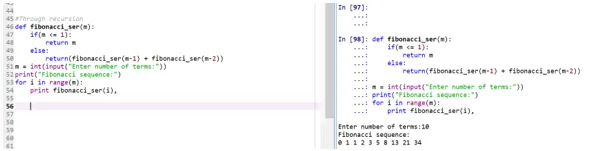
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
изход:
- Функцията „alig_ser“ отправя призив към себе си за отпечатване на серията Фибоначи.
- И оттук методът получи името си „рекурсия“.
Следващи стъпки:
- Тук потребителят е помолен да въведе мястото, до което трябва да се отпечата серията на Фибоначи.
- Числото преминава през функцията „Weight_ser“.
- Условието се проверява, ако предоставената дължина е по-малка от 1 или не. Ако да, резултатът се дава незабавно.
- Ако обаче дължината е по-голяма от 1, се правят рекурсивни обаждания към „vred_ser“ с аргументи с дължина, по-малка от 1 и 2, т.е.
- Следователно, рекурсията дава желания изход и го отпечатва.
- И така, накратко, Обсъдихме три начина за показване на серията Фибоначи.
- През за контур, през генератори и чрез рекурсия.
Всички три Python Code са обобщени
По-долу са трите python кода:
1. Чрез генератори
Код:
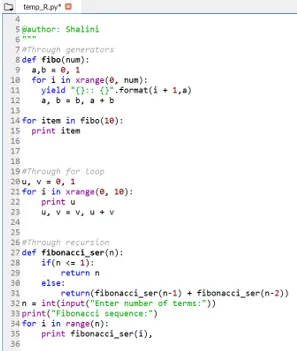
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Чрез за контур
Код:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Чрез рекурсия
Код:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Обобщено по-горе са всички процедури, човек трябва да практикува, за да се захване добре.
изход:
заключение
Преминавайки по-горе съдържанието на Фибоначи, човек би имал кристално ясно разбиране на числата и сериите на Фибоначи, специализирани с питон. Веднъж човек се чувства удобно с логиката на серията Фибоначи, генерирането на друг набор от серии, работата с други числа и с различни методи вече ще бъде преглед за вас. Логическият подход е единственият начин да се постигне превъзходство в това.
Препоръчителни статии
Това е ръководство за Фибоначи серия в Python. Тук обсъждаме числата и сериите на Фибоначи, специализирани с python, генериране на друг набор от серии, работа с други числа и с различни методи. Можете също да прегледате и другите ни свързани статии, за да научите повече -
- Генератор на случайни числа в Python
- Математически функции в Python
- Факториал в Python
- Капсулиране в Python
- Серия Фибоначи в Java
- Функции на Python
- Факторна програма в JavaScript
- Генератор на случайни числа в Matlab
- Генератор на случайни числа в C #
- Капсулиране в JavaScript