Въведение в алгоритма на йерархичната клъстеризация
Алгоритъмът на йерархичното клъстериране е техника, която не се контролира от машинно обучение. Тя има за цел да намери естествено групиране въз основа на характеристиките на данните.
Алгоритъмът на йерархичното клъстериране има за цел да намери вложени групи от данни чрез изграждане на йерархията. Той е подобен на биологичната таксономия на растителното или животинското царство. Йерархичните клъстери обикновено са представени с помощта на йерархичното дърво, известно като дендрограма.
Видове алгоритъм на йерархична клъстеризация
Йерархичните алгоритми за клъстериране са от два типа:
- разединителните
- Agglomerative
1. Разделителни
Това е подход отгоре надолу, при който първоначално се разглеждат всички данни като една група, а след това итеративно разделя данните на подгрупи. Ако е известен броят на йерархичен алгоритъм за клъстериране, тогава процесът на разделяне спира, след като се постигне броят на клъстерите. Освен това процесът спира, когато данните не могат да бъдат повече разделени, което означава, че подгрупата, получена от текущата итерация, е същата като тази, получена от предишната итерация (може също така да се счита, че делението спира, когато всяка точка от данни е клъстер ).
2. Агломеративен
Това е подход отдолу нагоре, който разчита на обединяването на клъстери. Първоначално данните са разделени на m единични клъстери (където стойността на m е броят на пробите / точките от данни). Два клъстера са обединени в един итеративно, като по този начин се намалява броят на клъстерите във всяка итерация. Този процес на обединяване на клъстери спира, когато всички клъстери са обединени в един или е постигнат броят на желаните клъстери.
На ниво 1 има m клъстери, които се свеждат до 1 клъстер на ниво m. Тези точки от данни, които се обединяват, за да образуват клъстер на по-ниско ниво, остават в същия клъстер и на по-високите нива. Например, да предположим, че има 8 точки x1..x8, така че първоначално има 8 клъстера на ниво 1. Да предположим, че точки x1 и x2 се сливат в клъстер на ниво 2, след това до ниво 8, те остават в същия клъстер.
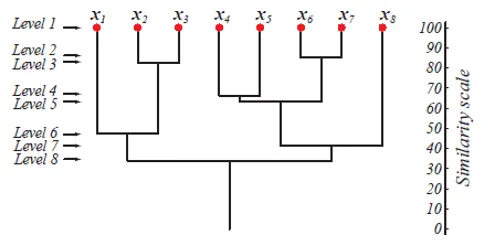
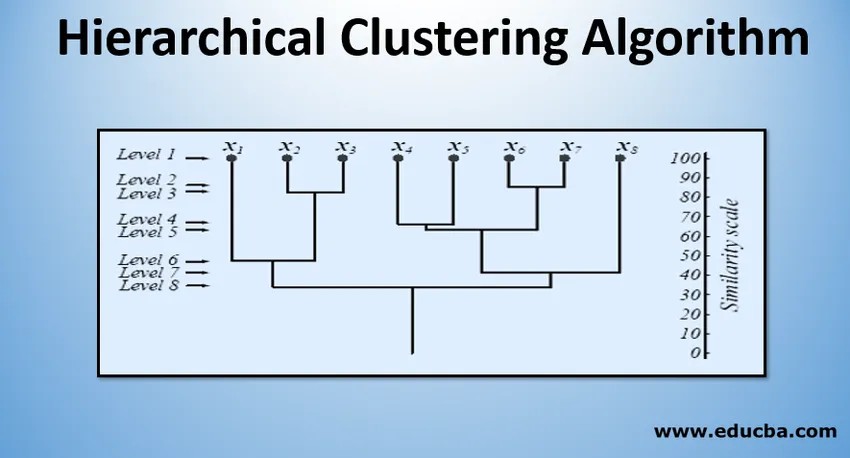
Горната фигура показва дендрограмно представяне на подхода за групиране на агломерация за 8 точки от данни, както и скалата на прилика, съответстваща на всяко ниво.
Нивата на клъстерите ни дават представа колко подобни са точките от данни в клъстерите. Както е показано на фигура 1, по-рано точките от данни се обединяват в клъстер, подобни са. Така че точките от данни в клъстер на ниво 2 (напр. Х2 и х3) са по-сходни от тези точки от данни в клъстер на ниво 6 (напр. Х1 и х2).
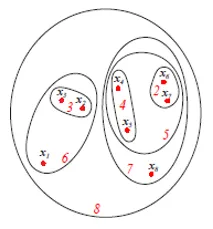
Горната фигура показва представяне на диаграмата Set или Venn на агломеративния подход за клъстериране на горепосочените 8 точки от данни. Дендрограмите и зададените представи могат да се използват за клъстеризиране. Въпреки това, дендрограмата обикновено е за предпочитане представяне на активи не може количествено да представи сходството на клъстера.
Стъпки за йерархичен алгоритъм на клъстериране
Нека следваме следните стъпки за алгоритъма на йерархичното клъстериране, които са дадени по-долу:
1. Алгоритъм
Алгоритъм за агломеративен йерархичен клъстер
- Започнете инициализирайте c, c1 = n, Di = (xi), i = 1, …, n '
- Направете c1 = c1 - 1
- Намерете най-близките клъстери, да речем Di и Dj
- Сливане на Di и Dj
- Докато c = c1
- Връщане c клъстери
- Край
Този алгоритъм започва първо с n клъстера, където всяка точка от данни е клъстер. С всяка итерация броят на клъстерите намалява с 1, тъй като двете най-близки клъстери се обединяват. Този процес продължава, докато броят на клъстерите не се намали до предварително зададената стойност c.
Как да решите кои клъстери са в близост?
Това се дефинира с помощта на няколко показателя за разстояние, които са както следва:
- Минималното разстояние между клъстерите dmin (Di, Dj). Полезно за единично.
- Максималното разстояние между клъстерите dmax (Di, Dj). Полезно за пълно.
- Средното разстояние между клъстерите davg (Di, Dj).
Какво е единична и пълна връзка?
- Когато dmin (di, dj) се използва за намиране на разстоянието между два клъстера и алгоритъмът се прекратява, ако разстоянието между най-близките клъстери надвишава прага, тогава алгоритъмът се нарича алгоритъм на една връзка.
- Когато dmax (Di, Dj) се използва за намиране на разстоянието между два клъстера и алгоритъмът се прекратява, ако разстоянието между най-близките клъстери надвишава прага, тогава алгоритъмът се нарича пълен алгоритъм за свързване.
- Нека разгледаме всяка точка от данни като възел на графика. Има граница между две точки от данни, ако те принадлежат на един и същ клъстер. Когато се обединят два най-близки клъстера, се добавя ръб. Тя се нарича единична връзка, тъй като съществува уникален път от един възел до другия.
- Пълният алгоритъм за свързване обединява два клъстера, като минимизира разстоянието между двете най-отдалечени точки.
- Един алгоритъм за свързване генерира обхващащо се дърво. Този алгоритъм обаче е податлив на шум. Пълният алгоритъм за свързване генерира пълна графика.
Каква е времевата сложност на алгоритъма?
Да предположим, че имаме n модели в двумерното пространство и използваме dmin (Di, Dj), за да образуваме c клъстери. Трябва да изчислим n (n - 1) междусекторни разстояния - всяко от които е изчисление O (d 2 ) - и да поставим резултатите в таблица на разстоянията между точки. Космическата сложност е O (n 2 ). Намирането на двойката с минимално разстояние (за първото сливане) изисква да преминем през пълния списък, запазвайки индекса на най-малкото разстояние.
По този начин за първия агломеративен етап сложността е O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). За друг произволен етап на агломерация (т.е. от c1 до c1 - 1), ние просто преминаваме през n (n - 1) - c1 „неизползвани“ разстояния в списъка и намираме най-малкото, за което x и x 'лежат в различни клъстери, Това отново е O (n (n − 1) −c1). Следователно общата времева сложност е O (cn 2 d 2 ), а при типични условия n >> c.
2. Визуализация
След като данните се разделят на клъстери, е добра практика да се визуализират клъстерите, така че да се добие представа как изглежда групирането. Но визуализирането на тези данни с големи размери е трудно. Затова използваме анализ на главни компоненти (PCA) за визуализация. След PCA получаваме точките от данни в нискомерното пространство (обикновено 2D или 3D), които можем да начертаем, за да видим групирането.
Забележка: Висока размерност означава голям брой функции, а не брой точки от данни.3. Оценка
Един от методите за оценка на клъстерите е, че разстоянието на точките между клъстерите (междукластерното разстояние) трябва да бъде много повече от разстоянието на точките в клъстера (интракластерно разстояние).
заключение
Следват няколко ключови начина:
- Йерархичният алгоритъм за клъстериране се използва за намиране на вложени модели в данните
- Йерархичното клъстериране е от 2 вида - разделително и агломеративно
- Dendrogram и set / Venn диаграма могат да се използват за представяне
- Единичната връзка обединява два клъстера, като свежда до минимум минималното разстояние между тях. Образува разпръскване
- Пълната връзка обединява два клъстера, като свежда до минимум максималното разстояние между нея.
- Общата времева сложност на йерархичния алгоритъм за клъстериране е O (cn 2 d 2 ), където c е предварително зададеният брой клъстери, n е броят на моделите и d е двумерното пространство на n моделите.
Препоръчителни статии
Това е ръководство за алгоритъма на йерархичните клъстери. Тук обсъждаме видовете и стъпките на йерархичните алгоритми за клъстериране. Можете също да разгледате следните статии, за да научите повече-
- Йерархичен анализ на клъстеринга
- Йерархична клъстеризация в R '
- Алгоритъм на клъстеризация
- Какво е клъстеризиране в Data Mining?
- Йерархично клъстериране | Агломеративно и разделно клъстеризиране
- C ++ Алгоритъм | Примери за C ++ алгоритъм