Въведение в йерархичното клъстериране
- Наскоро един от нашите клиенти поиска от нашия екип да представи списък на сегментите с ред на важност за клиентите им, за да ги насочи към франчайзинг на един от новите им продукти. Ясно е, че само сегментирането на клиентите, използващи частично клъстериране (k-означава, c-размито), няма да изведе ред на важност, където иерархичното клъстериране влиза в картината.
- Йерархичното клъстериране е разделяне на данните в различни групи въз основа на някои мерки за сходство, известни като клъстери, което по същество е насочено към изграждането на йерархията между клъстерите. По същество е неподдържаното обучение и избирането на атрибутите за измерване на сходството е специфично за приложението.
Йерархията на клъстера на данни
- Агломеративно клъстеризиране
- Разделяне на клъстеринг
Нека вземем пример с данни, оценки, получени от 5 ученици, за да ги групираме за предстоящо състезание.
| Студент | Marks |
| А | 10 |
| B | 7 |
| ° С | 28 |
| д | 20 |
| E | 35s |
1. Агломеративно клъстеризиране
- Като начало ние считаме, че всяка отделна точка / елемент тук тежи като клъстери и продължаваме да обединяваме подобни точки / елементи, за да образуваме нов клъстер на новото ниво, докато не ни остане единичният клъстер е подход отдолу нагоре.
- Единична връзка и цялостна връзка са два популярни примера за агломеративно групиране. С изключение на тази Средна връзка и Центроидна връзка. В едно свързване ние обединяваме във всяка стъпка двата клъстера, чиито два най-близки члена имат най-малкото разстояние. При пълно свързване ние се сливаме в членовете на най-малкото разстояние, които осигуряват най-малкото максимално двойно разстояние.
- Матрица на близост, Тя е ядрото за извършване на йерархично клъстериране, което дава разстоянието между всяка от точките.
- Нека направим матрица за близост за нашите данни, дадени в таблицата, тъй като изчисляваме разстоянието между всяка от точките с други точки, това ще бъде асиметрична матрица с форма n × n, в нашия случай 5 × 5 матрици.
Популярен метод за изчисляване на разстоянието са:
- Евклидово разстояние (квадрат)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Разстояние от Манхатън
dist((x, y), (a, b)) =|x−c|+|y−d|
Най-често се използва евклидово разстояние, тук ще използваме същото и ще преминем със сложна връзка.
| Student (клъстери) | А | B | ° С | д | E |
| А | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| ° С | 18 | 21 | 0 | 8 | 7 |
| д | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Диагоналните елементи на матрицата за близост винаги ще са 0, тъй като разстоянието между точката със същата точка ще бъде винаги 0, следователно диагоналните елементи са освободени от разглеждане за групиране.
Тук в итерация 1 най-малкото разстояние е 3, следователно ние обединяваме A и B, за да образуваме клъстер, отново образуваме нова матрица за близост с клъстер (A, B), като вземем (A, B) клъстерна точка като 10, т.е. максимум от ( 7, 10), така че новообразуваната матрица за близост ще бъде
| клъстерите | (A, B) | ° С | д | E |
| (A, B) | 0 | 18 | 10 | 25 |
| ° С | 18 | 0 | 8 | 7 |
| д | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
В итерация 2, 7 е минималното разстояние, следователно ние сливаме C и E, образувайки нов клъстер (C, E), повтаряме процеса, последван в итерация 1, докато не приключим с единичния клъстер, тук спираме на итерация 4.
Целият процес е изобразен на фигурата по-долу:
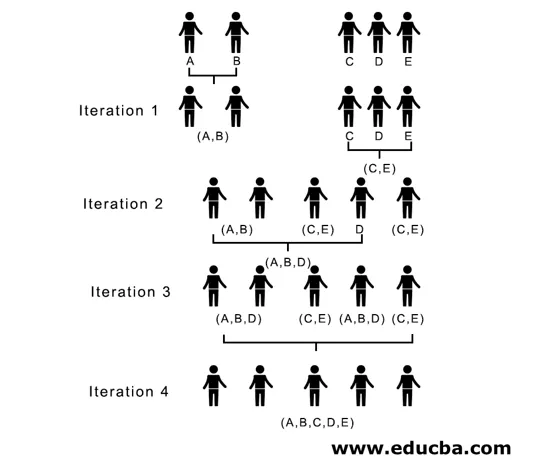
(A, B, D) и (D, E) са двата клъстера, образувани при итерация 3, при последната итерация можем да видим, че ни остава един единствен клъстер.
2. Разделяне на клъстеринг
Като начало считаме всички точки за един клъстер и ги разделяме на най-далечно разстояние, докато не приключим с отделни точки като отделни клъстери (не е задължително да спрем в средата, зависи от минималния брой елементи, които искаме във всеки клъстер) на всяка стъпка. Това е точно обратното на агломеративното групиране и е подход отгоре надолу. Разделящото клъстериране е начин, който се повтаря k означава групиране.
Изборът между агломеративно и разделно клъстериране отново зависи от приложението, но няколко точки, които трябва да се вземат предвид, са:
- Разделянето е по-сложно от агломеративното групиране.
- Разделеното клъстериране е по-ефективно, ако не генерираме пълна йерархия до отделни точки от данни.
- Агломеративното клъстериране взема решение, като обмисля локалните карти, без да се вземат предвид глобалните модели, които първоначално не могат да бъдат обърнати.
Визуализация на йерархичното клъстериране
Супер полезен метод за визуализиране на йерархично клъстеризиране, който помага в бизнеса е Dendogram. Дендограмите са дървовидни структури, които записват последователността на сливания и разцепления, при които вертикалната линия представлява разстоянието между струпванията, разстоянието между вертикалните линии и разстоянието между клъстерите е пряко пропорционално, т.е.
Можем да използваме дендограмата, за да определим броя на клъстерите, просто да начертаем линия, която се пресича с най-дългата вертикална линия на дендограмата, редица пресечени вертикални линии ще бъдат броят на клъстерите, които ще бъдат разгледани.
По-долу е примерът Dendogram.
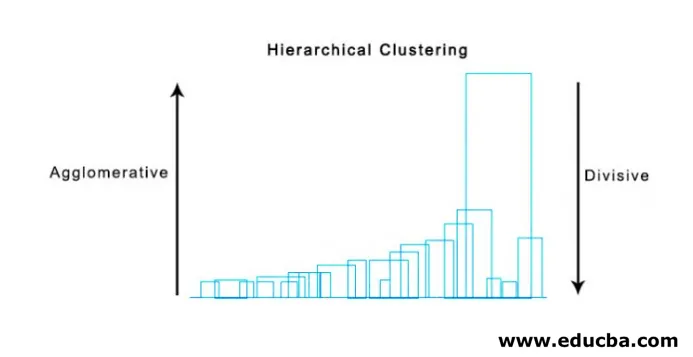
Има доста прости и директни пакети на python и функциите му да изпълняват йерархично клъстериране и графични дендограми.
- Йерархията от науката.
- Cluster.hierarchy.dendogram за визуализация.
Общи сценарии, в които се използва йерархична клъстеризация
- Сегментиране на клиента към маркетинг на продукти или услуги.
- Градско планиране за идентифициране на местата за изграждане на структури / услуги / сгради.
- Анализ на социалните мрежи, например, идентифицира всички фенове на MS Dhoni, за да рекламират биографията му.
Предимства на йерархичното клъстериране
Предимствата са дадени по-долу:
- В случай на частично клъстериране като k-средства, броят на клъстерите трябва да бъде известен преди кластеризирането, което не е възможно в практическите приложения, докато при йерархичното клъстеризиране не се изисква предварително знание за броя на клъстерите.
- Йерархичното клъстериране извежда йерархия, т.е. структура, по-информативна от неструктурирания набор от плоските клъстери, върнати чрез частично клъстериране.
- Йерархичното клъстеризиране е лесно за изпълнение.
- Представя резултати в повечето от сценариите.
заключение
Типът на клъстериране прави голямата разлика при представянето на данни, като йерархичното клъстериране е по-информативно и лесно за анализиране е по-предпочитано от частичното клъстериране. И често се свързва с топлинни карти. Да не забравяме атрибутите, избрани за изчисляване на сходство или различие, влияят предимно както на клъстерите, така и на йерархията.
Препоръчителни статии
Това е ръководство за йерархично клъстеризиране. Тук обсъждаме въвеждането, предимствата на йерархичното клъстериране и общите сценарии, в които се използва йерархично клъстериране. Можете също да прегледате и другите ни предложени статии, за да научите повече -
- Алгоритъм на клъстеризация
- Клъстеризиране в машинно обучение
- Йерархична клъстеризация в R
- Методи на клъстериране
- Как да премахнете йерархията в Tableau?