Excel Linear Interpolation (Съдържание)
- Какво е интерполация?
- Интерполация с функция за прогнозиране в Excel
- Примери за линейна интерполация в Excel
Какво е интерполация?
В света на математиката интерполацията е метод за създаване на нови точки от данни с помощта на известни точки от данни. Интерполацията оценява стойността въз основа на съществуващите налични стойности на данни, които могат да бъдат относими.
Например - ако караме колело със скорост 60 км / час и достигаме определена дестинация за 1 час и ако караме с 45 км / час и достигаме определена дестинация за 45 минути. И така, колко време ще отнеме, за да стигнем до дестинация, ако караме със скорост 30 км / час.
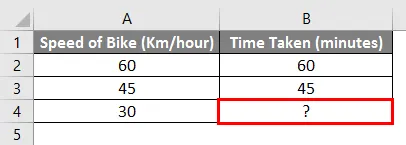
Използвайки проста математика, можем да изчислим липсващите стойности в горния пример. Трябва да вмъкнем по-долу формулата в клетка В4.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
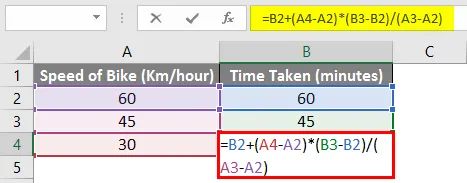
Така че въз основа на горната формула можем да кажем, че са нужни 30 минути, за да стигнем до дестинацията, ако караме със скорост 30 км / час.
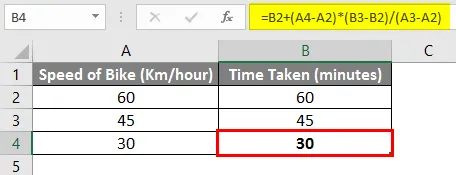
Нека се опитаме да разбием горната формула и да разберем формулата подробно.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
В горния пример последният раздел от формулата, който е маркиран с червено, изчислява колко време се променя, когато скоростта на мотора се промени с 1. В нашия пример времето, което се променя, се променя с 1 минута, когато скоростта на мотора се променя с 1 км / час.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Вторият раздел (в син цвят по-горе) изчислява колко далеч е скоростта на мотора ни от първата дадена скорост на мотора, след което го умножава по стойността, изчислена по-горе. Въз основа на нашия пример е 30 (Cell A4) минус 60 (Cell A2), резултатът от което се умножава по 1 (което е равно на -30).
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
И накрая, първият раздел на формулата (в кафяво по-горе); добавяме първата стойност на скоростта на мотора. В нашия пример това осигурява крайния резултат от 60 + (-30) * (1) = 30 минути. В училище използвахме формулата по-долу, за да изчислим липсващата стойност на Y.
Y = Y1 + (X-X1) * (Y2-Y1) / (X2 - X1)
Това е пример за това как да се изчислят липсващите стойности с помощта на ръчна формула, за да се разбере интерполацията.
Excel има вградена функция, която прави подобно изчисление като по-горе и е известно като FORECAST функция. Сега ще научим подробно тази функция.
Интерполация с функция за прогнозиране в Excel
Прогнозата е функция на работен лист, налична в MS Excel и използва линейна регресия, за да открие липсващата стойност. Прогноза, както и името му подсказва, че се използва за прогнозиране на бъдещата стойност на точка от данни, но може да се използва и за интерполиране на стойност. По принцип се използва за изчисляване на бъдещата стойност въз основа на съществуващите стойности на конкретен набор от данни.
Синтаксис на функция за прогнозиране

Аргументи на прогнозната функция:
- x - Това е точка от данни, за която искаме да знаем резултиращата стойност.
- K known_y's - Обхват от клетки, съдържащи стойностите на Y.
- K known_x's - Обхват от клетки, съдържащи стойностите на X.
Сега като разгледаме същия горепосочен пример, нека се опитаме да използваме функцията за прогнозиране.
В нашия пример,
x - клетка B4 (тъй като искаме да разберем времето, отнесено при скорост в 30 км / час).
K known_y's - Cell B2 to Cell B3 (Време, взето за известната скорост на мотора).
K known_x's - Cell A2 to Cell A3 (Скорост на вече даден мотор, за който знаем времето, отведено).
Така че крайната формула в клетка В4 ще бъде както следва:
= ПРОГНОЗА (А4, В2: B3, A2: A3)
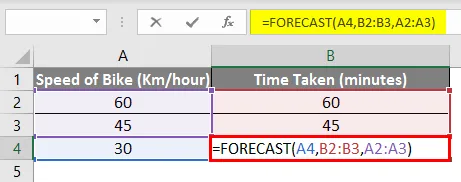
И както виждате, крайният резултат е същият, т.е. 30 минути .
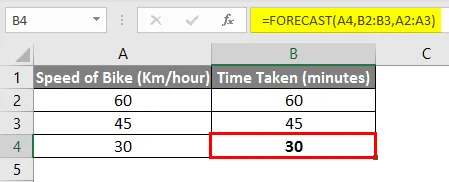
За да създадете диаграма, отидете на менюто Вмъкване, щракнете върху Скатер и след това изберете Скатер с гладки линии и маркери.
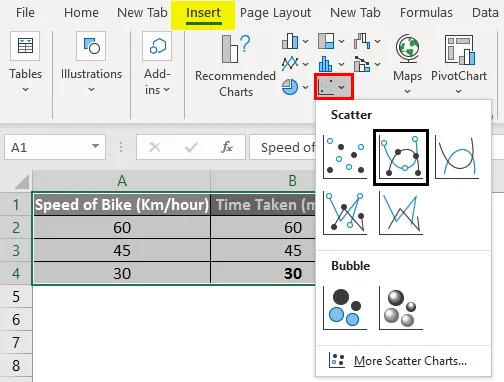
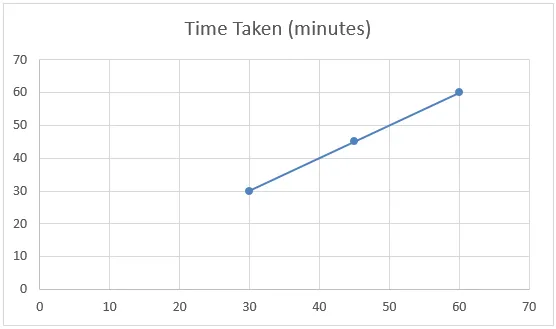
Ако разгледаме таблицата по-долу от горния пример, можем да кажем, че наборът от данни има линейна връзка и известен като линейна интерполация.
Примери за линейна интерполация в Excel
Нека разберем линейната интерполация в Excel с някои примери.
Можете да изтеглите този шаблон за линейна интерполация на Excel тук - линеен шаблон на Excel ExcelПример №1
Да предположим, че имате данни за продажбите и печалбата за предходни години и искате да знаете печалбата на текущата година, ако постигнете определено ниво на продажби.
Погледнете таблицата по-долу. Имате данни за продажбите от 2016 до 2018 г. и искате да знаете каква трябва да бъде печалбата, ако продажбите ви са Rs. 40, 00 000 през 2019г.
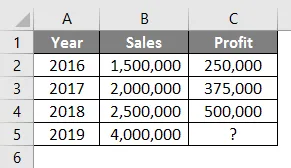
Така че с помощта на функцията за прогнозиране можем да интерполираме печалбата на 2019 г., когато продажбите са Rs. 4000000
Формулата в клетка C5 ще бъде както следва:
= Прогноза (B5, C2: C4, B2: B4)
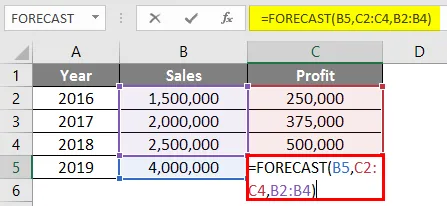
След използване на формулата за прогноза отговорът е показан по-долу.
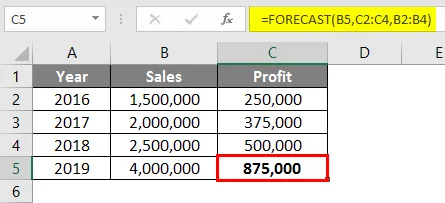
Резултатът за функцията за прогнозиране ще бъде Rs. 875 000 въз основа на данните за продажбите и печалбата, налични от 2016 до 2018 година.
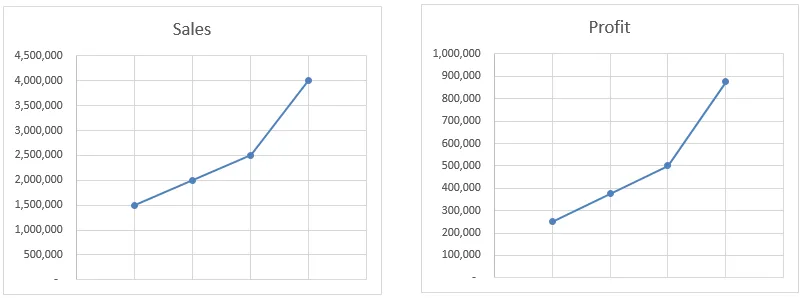
В този пример функцията за прогнозиране интерполира стойността въз основа на всички налични данни, а не само начална и крайна точка. Както можете да видите в диаграмите, печалбата се движи е абсолютно същата като продажбите. Дори да изчислим стойността ръчно, тя все пак ще ни даде същия резултат.
Пример №2
Имаме данни за последните 9 мача на отбора по крикет, който е изминал пирони и е изпълнен с отбори.
Искаме да разберем колко писти ще отбележат отборите, ако паднат 8 уикита.
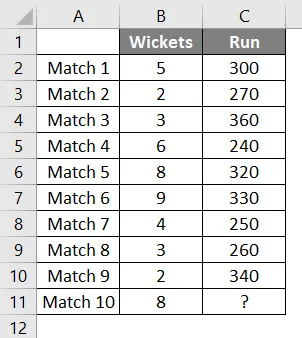
Така че отново ще използваме същата функция за прогнозиране, както по-горе.
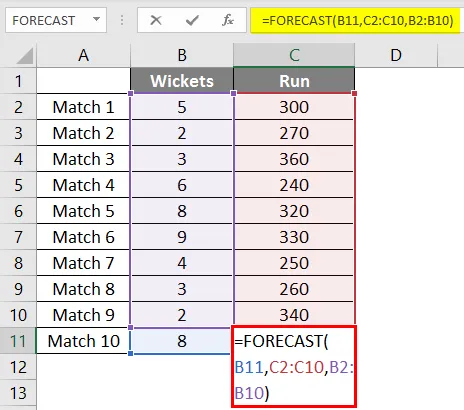
След като приложим формулата, получаваме резултата от 302 руна, ако 8 отбрани падаме въз основа на линейна регресия на последните 9 мача, изиграни от екипа.
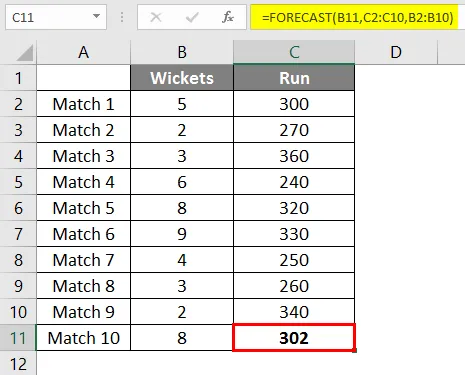
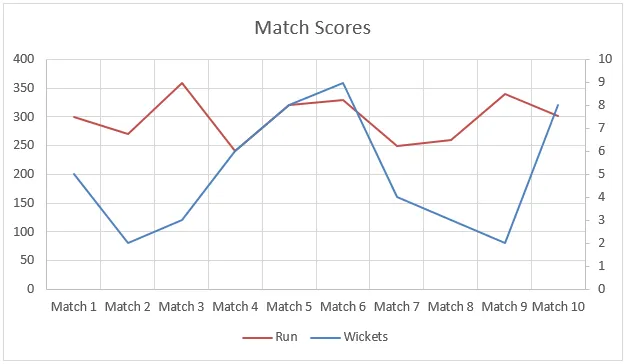
В този пример данните не са линейни и можете да видите това в графиката по-долу. Но все пак функцията прогноза ни помогна да интерполираме пистите с помощта на данни от предишни мачове.
Неща, които трябва да запомните за линейната интерполация в Excel
- Функцията за прогнозиране се използва за прогнозиране / оценка на стойността въз основа на съществуващите налични стойности, но също така може да помогне за интерполиране на липсващата стойност.
- В случай, че данните не са линейни, функцията за прогнозиране няма да ви даде точната стойност, която се основава на линейна интерполация, но ще ви даде най-близката стойност.
- Ако x във функцията за прогнозиране е текстова или нецифрена, функцията прогноза връща грешката #VALUE.
- Ако Kknown_x и Kknown_y's не съдържа никакви данни или съдържа различен набор от точки от данни, функцията за прогнозиране ще даде грешка # N / A.
- Ако дисперсията на K known_x е нула, функцията прогноза дава грешка # DIV / O.
Препоръчителни статии
Това е ръководство за линейна интерполация в Excel. Тук обсъждаме как да използваме линейна интерполация в Excel, заедно с практически примери и шаблон за excel за сваляне. Можете да разгледате и другите ни предложени статии -
- Линейна регресия в Excel
- Търсене на текст в Excel
- Текстова формула в Excel
- Marimekko Chart Excel
- Интерполирайте в Excel
- Линейно програмиране в Excel