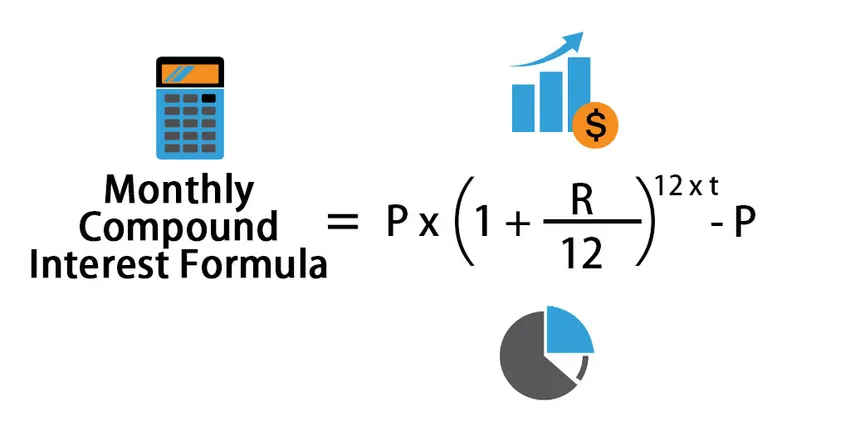
Месечна формула за сложни лихви (Съдържание)
- формула
- Примери
- калкулатор
Каква е месечната формула за сложна лихва?
Когато определена сума пари е взета назаем за определена продължителност, и допълнителна сума трябва да се раздели заедно с заемната сума. Тогава допълнителната сума, която плащаме по фиксирания лихвен процент, се нарича като лихва. Сложната лихва е общата лихва, която включва първоначалната лихва и лихвата на новата главница, която се развива чрез добавяне на първоначалната главница към дължимата лихва. За изчисляване на месечно изчисляване на лихвата, която се усложнява през целия месец през цялата година.
Месечната формула на сложната лихва може да се изчисли като:
Monthly Compound Interest Formula = P * (1 + (R /12)) 12*t – P
където,
- P = главна сума
- R = процент
- t = Време
Примери на месечна формула за сложен интерес (с шаблон на Excel)
Нека вземем пример, за да разберем по-добре изчислението на месечната сложна лихва.
Можете да изтеглите този месечен шаблон на формула за формулировка на сложните лихви тук - Ежемесечен шаблон за формула на сложен интерес ExcelМесечна формула за лихва на съединение - Пример №1
Кредитополучателят е взел назаем сума от 10 000 руски при ставка 8%. Изчислете месечния сложен лихвен процент за 2 години?
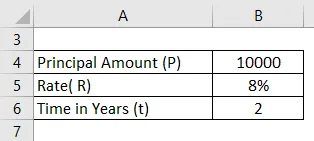
Решение:
Месечната лихва за съединение се изчислява по формулата, дадена по-долу
Месечна лихва за съединение = P * (1 + (R / 12)) 12 * t - P
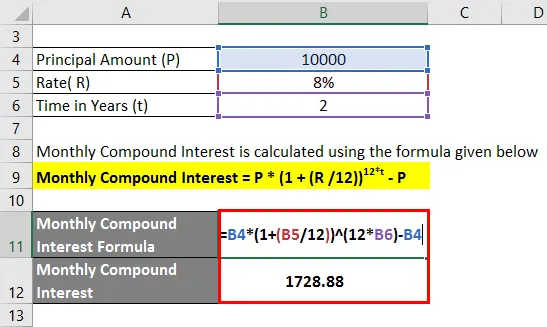
- Месечна лихва за съединение = 10 000 (1 + (8/12)) 2 * 12 - 10 000
- Месечна лихва за съединение = 1, 728.88
Месечната сложна лихва за 2 години е 1, 728.88 Rs
Месечна формула за лихва на съединение - пример №2
Сума пари, инвестирана при 10% е 20 000 Rs. Каква ще бъде месечната сложна лихва за 10-те години?

Решение:
Месечната лихва за съединение се изчислява по формулата, дадена по-долу
Месечна лихва за съединение = P * (1 + (R / 12)) 12 * t - P
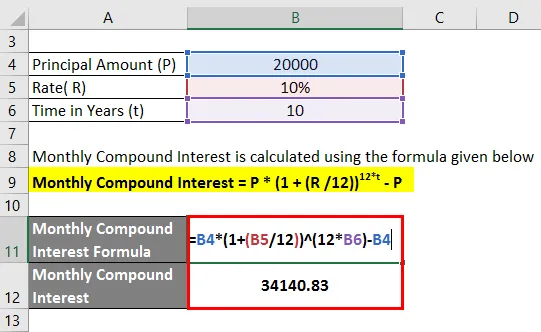
- Месечна сложна лихва = 20 000 (1 + 10/12)) 10 * 12 - 20 000
- Месечна лихва за съединение = 34 140, 83
Месечната сложна лихва за 10 години е 34 140, 83 Rs
Месечна формула за лихва на съединение - Пример №3
Г-жа Джеферсън купи античен статут за 500 долара. Пет години по-късно тя продаде този статус за 800 долара. Тя го смяташе за част от инвестицията. Изчислете годишната ставка, която е получила?
Решение:
Ако помислим за инвестиция от 500 долара и получаваме 800 долара в бъдещия период от време след t = 10 години. Приемаме годишна норма m = 1 и я прилагаме във формулата.
A = P (1 + r / m) mt
- 800 = 500 (1+ r / 1) 1 * 10
- 800 = 500 (1 + r) 10
Сега ние решаваме за Rate (r) в следващите стъпки.
- 800 = 500 (1 + r) 10
- 8/5 = (1 + r) 10
Сега взимаме силата на (1/10) от лявата страна на уравнението и изчистваме от дясната страна.
- (8/5) 1/10) = 1 + r
Изчислете стойността отляво и решете за r.
- 1.0481 = 1 + r
- 1.0481 - 1 = r
- 0, 0481 = r
Г-жа Джеферсън обаче спечели годишния лихвен процент от 4, 81%, което не е лоша доходност.
обяснение
Сложната лихва е произходът от първоначалната сума на главницата с един плюс годишната лихва, увеличена до броя на сложните периоди минус един. Така първоначалната сума на заема след това се изважда от получената стойност.
Сложната лихва може да се изчисли като:
Формула за сложна лихва = (P (1 + i) n ) - P
Формула за сложна лихва = (P (1 + i) n - 1)
Където:
- P = главна сума
- i = годишна лихва в проценти
- n = Периоди на усложняване
Има определен набор от процедури, чрез които можем да изчислим месечната сложна лихва.
Стъпка 1: Ние трябва да изчислим размера на лихвата, получена чрез използване на месечна компенсация. Формулата може да се изчисли като:
- A = (P (1 + i) n - 1) - P
Стъпка 2: ако приемем, че лихвеният процент е 5% годишно. На първо място, трябва да изразим стойността на лихвения процент в еквивалентното десетично число. Това може да стане по следния начин.
- 5% = 5/100 = 0, 05
Стъпка 3: Тъй като знаем, че лихвата се усложнява месечно, така че можем да вземем n = 12. Въпреки това, в този случай е посочен периодът от време, ние считаме, че заемът е взет за период от една година. Сега имаме всички променливи на разположение при нас, които можем директно да заместим във формулата и да получим резултата от нея.
- A = 1000 ((1 + 0, 05 / 12) 12 - 1)
- A = 1000 ((1 + 0, 0042) 12 - 1)
- A = 1000 ((1.0042) 12 - 1)
- A = 1000 (1.0516 - 1)
- A = 1000 (0, 0516)
- A = 51.6
Изчислихме лихвения процент за 1 година, като месечните компенсации са около 51.6
Месечната сложна лихва не отразява забележими промени, когато паркираме определена сума пари за краткосрочна продължителност. Причината е, че отнема няколко години, за да се добавят забележими промени в действие.
И най-забележителното в сложния интерес е, че той прави вашите инвестиции да растат по-бързо от обикновените лихви. Колкото по-чести са интервалите ви за комбиниране, толкова по-голяма е разликата или можем да кажем, че ежедневната лихва за комбиниране генерира повече приходи от вашите инвестиции, отколкото годишната сложна лихва за всеки даден лихвен процент.
Следващата таблица показва разликата, че броят на усложняващите се периоди може да направи за определен период от време за заем от 10 000 долара с годишна лихва от 10% за 12-годишен период.
| Сложна честота | Брой на сложните периоди | Стойности за i и n | Обща лихва |
| ежегодно | 1 | I = 10%, n = 12 | $ 21, 384.2837 |
| Полу годишно | 2 | I = 5%, n = 24 | $ 22, 250.9994 |
| тримесечен | 4 | I = 2, 5%, n = 48 | $ 22, 714.8956 |
| Месечно | 12 | I = 0, 833%, n = 144 | $ 23, 036.4896 |
Съответствие и използване на формулата за месечна сложна лихва
Сложната лихва се оказа по-добрият инструмент за инвестиции, но може да бъде много опасен, ако е приложим за размера на вашия заем. В крайна сметка ще плащате повече лихва върху сумата на вашия заем.
Съчетаването става по-ефективно, когато вашата инвестиция е или месечна, или тримесечна, вместо годишна, защото дава по-добра възвръщаемост. Ако заемате пари от някоя от банката или финансовата институция, най-добрият вариант е годишното събиране. Когато заемате определена сума пари, тогава ежедневното смесване ще бъде по-продуктивно. Но трябва да имаме предвид, че съставянето може да бъде благоприятно или неблагоприятно да зависи от обстоятелствата.
Сложната лихва дава по-добра възвръщаемост на вашата инвестиция, зависи от срока и размера на инвестицията. Сложният интерес расте по-бързо от вашите очаквания.
Ползите от сложната лихва са изброени по-долу:
- повторно инвестиране
- По-добра възвръщаемост на вашата инвестиция.
- Дългосрочни спестявания.
- Увеличена печалба.
Месечен калкулатор на формула за сложна лихва
Можете да използвате следния калкулатор на формула за месечна сложна лихва
| P | |
| R | |
| T | |
| Месечна формула за сложна лихва | |
| Месечна формула за лихва на сложна лихва = | P x ((1 + R / 12) 12 * t - P) |
| = | 0 x ((1 +0/12) 12 * 0 - 0) = 0 |
Препоръчителни статии
Това е ръководство за месечната формула за сложни лихви. Тук обсъждаме как да изчислим формулата за месечна сложна лихва заедно с практически примери. Ние също така предлагаме месечен калкулатор за сложни лихви с изтеглящ се шаблон за excel. Можете също да разгледате следните статии, за да научите повече -
- Формула за съставен годишен темп на растеж
- Как да изчислим номиналната лихва?
- Ежедневна формула за сложна лихва
- Ръководство за формулата за разпределение на Poisson
- Лихва срещу дивидент | Топ 8 ключови разлики, които трябва да знаете